Riesci a fermare il virus e risolvere l’indovinello?

Nell'indovinello del virus, un gruppo di scienziati deve riuscire a capire come fermare un pericolossimo virus preistorico. L’unico modo che hanno per evitare che si diffonda ovunque è distruggere una ad una tutte le stanze del proprio laboratorio riempiendole di un liquido tossico sia per il virus che per gli umani. Come faranno a salvare il mondo e a sopravvivere?

Questo indovinello, all’apparenza molto semplice, rimanda al problema del commesso viaggiatore, un famoso problema di ottimizzazione dei percorsi e degli algoritmi. Studiare questo tipo di situazioni non serve solo a stimolare la logica: è utile in ambiti come la logistica, l’informatica e l’organizzazione di reti e trasporti, dove pianificare percorsi efficienti è fondamentale.

Vediamo come risolverlo e cos’è il problema del commesso viaggiatore.

In cosa consiste l'indovinello del virus

Ci troviamo in questa situazione: il nostro team di ricerca ha scoperto un virus preistorico conservato nel permafrost e lo ha portato in laboratorio per studiarlo. Dopo una lunga giornata di lavoro, stiamo per chiudere tutto quando un terremoto improvviso fa saltare la corrente, sigillando i portelloni di sicurezza, sia interni che esterni. Appena riusciamo a riattivarla, scatta l’allarme: tutte le fiale contenenti il virus si sono rotte e il patogeno si è diffuso in quasi tutte le stanze.

Tra meno di mezz’ora, i condotti di aerazione si apriranno, spargendo il virus nel mondo. Per evitarlo, dobbiamo entrare in ogni stanza contaminata e attivare l’interruttore che avvia il protocollo di decontaminazione. Una volta attivato, abbiamo 10 secondi per fuggire nella stanza successiva, prima che quella in cui ci troviamo venga riempita di un liquido tossico per il virus e per gli umani. Dopo l’allagamento, tornare indietro non sarà più possibile.

Il laboratorio è composto da 16 stanze disposte a file da 4, tutte collegate tra loro da portelloni di sicurezza. C’è una sola stanza di ingresso e una di uscita, come mostrato nel disegno.

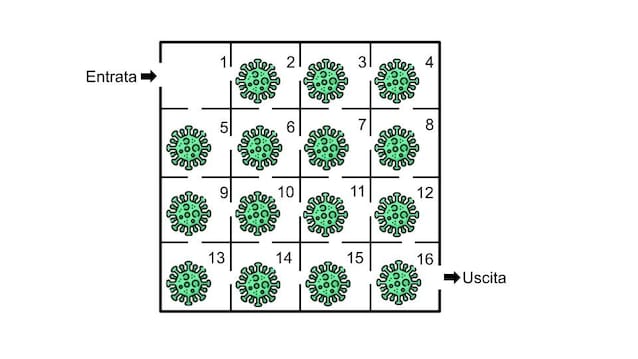
A questo punto, prendiamo i nostri taccuini, disegniamo la pianta del laboratorio e segniamo le stanze contaminate. Iniziamo a tracciare possibili percorsi sulla mappa, ma nessuno sembra portarci all’uscita senza saltare almeno una stanza. Sembra impossibile distruggere il virus ovunque e riuscire a salvarsi.

Per fortuna, nel team di ricerca c’è anche una brillante matematica che guarda la mappa e dice:

Meno male che il virus non ha contaminato anche la prima stanza, altrimenti non avremmo scampo.

Cos’ha capito? E come faremo a salvare il mondo?

La soluzione dell'indovinello del virus: la prima stanza non è contaminata

Partiamo dal punto chiave: come faremo a salvare il mondo? La nostra collega ha avuto l’intuizione giusta: dobbiamo sfruttare il fatto che la prima stanza non è ancora contaminata. Questo ci permette di spostarci una volta verso una delle stanze adiacenti e poi tornare indietro.

Scegliamo quindi di entrare nella stanza di fronte a noi, la numero 2, attivare l’interruttore e rientrare subito nella stanza 1. Ora la stanza 2 è distrutta, e quando abbiamo aperto il portellone tra la stanza 2 e la 1, anche la 1 si è contaminata. Quindi, schiacciamo l’interruttore anche nella stanza 1 e ci spostiamo verso la 5, l’unica vicino a noi rimasta intatta.

Da lì, possiamo continuare verso la 6 o verso la 9. In entrambi i casi esistono diversi percorsi che ci permettono di raggiungere l’uscita passando per tutte le stanze contaminate, come, ad esempio, quelli che vediamo nell'immagine.

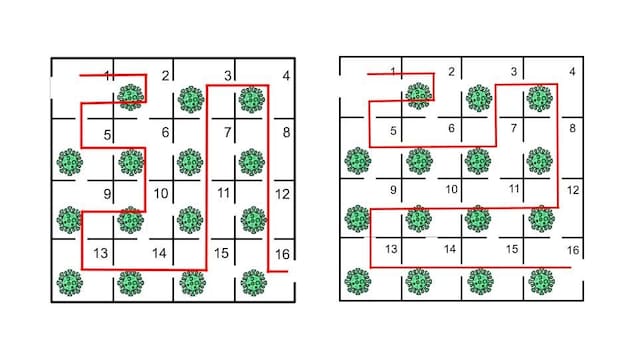
Riusciamo così a salvare il mondo da questo pericolosissimo virus e ad uscirne fuori sani e salvi.

Passare una volta sola per ogni punto: il problema del commesso viaggiatore

Trovare strategie per passare una volta sola da tutti i punti su una mappa non è solo un esercizio di logica, è anche importantissimo in ambiti come la logistica, l’informatica e l’organizzazione del trasporto pubblico. Pensiamo, ad esempio, di dover trovare il percorso migliore affinché un bus passi in tutti i punti nevralgici della città senza rifare più volte la stessa strada. Il ragionamento che faremo sarà molto simile a quello dell’indovinello! Questo tipo di problemi sono tutte varianti del “problema del commesso viaggiatore”, il più semplice e il più studiato tra i problemi di pianificazione dei percorsi e di gestione dei processi. Il nome arriva dalla formulazione del 1930, in cui si chiedeva:

Dato un elenco di città e le distanze tra ogni coppia di città, qual è il percorso più breve possibile che può percorrere un commesso viaggiatore per visitarle tutte esattamente una volta e ritornare alla quella di partenza?

I problemi di ottimizzazione, per quanto sembrino semplici quando si hanno pochi punti (o poche città) da cui passare, diventano incredibilmente complessi da risolvere quando il numero di punti aumenta, tanto che negli anni ‘60 un istituto di ricerca californiano offriva premi in denaro a chiunque fosse riuscito a risolvere almeno alcuni casi particolari.

Questi problemi non sono solo più difficili da risolvere quando aumentiamo il numero di punti, ma possono diventare addirittura impossibili se cambiamo alcune condizioni. Ad esempio, se nel nostro indovinello anche la prima stanza fosse stata contaminata, saremmo stati spacciati. Infatti, su una griglia da 4 righe e 4 colonne non esiste nessun percorso che inizi in alto a sinistra e finisca in basso a destra passando per tutte le stanze una sola volta … provare per credere.