La magia della costante di Kaprekar, il numero 6174 che torna sempre su sé stesso

La costante di Kaprekar, 6174, così chiamata in onore del matematico indiano Dattatreya Ramachandra Kaprekar che la scoprì, è un numero misterioso che torna sempre su se stesso. Se ordiniamo le sue cifre dalla più grande alla più piccola, e poi dalla più piccola alla più grande, otteniamo i numeri 7641 e 1476 che, sottratti l’uno dall’altro, danno di nuovo 6174. Ma non solo! Preso un qualunque numero di 4 cifre che siano tutte diverse tra loro – ad esempio 3520 – se scriviamo le sue cifre in ordine prima decrescente (5320) e poi crescente (0235), li sottraiamo e ripetiamo questo procedimento almeno sette volte prima o poi otterremo proprio 6174! È il cosiddetto algoritmo di Kaprekar. Si tratta di un procedimento che per i numeri di 4 cifre funziona così:

1. si parte da un numero, ad esempio 3520
2. si ordinano le cifre in ordine decrescente ottenendo un nuovo numero, 5320 nel nostro caso
3. si ordinano le cifre in ordine crescente ottenendo un nuovo numero, 0235 nel nostro caso
4. Si sottrae il numero piccolo al numero grande ottenendo un nuovo numero, 5320-0235=5085 nel nostro caso

Questo algoritmo può essere reiterato sul risultato ottenuto, tutte le volte che vogliamo, noi ad esempio siamo partiti da 3520 e possiamo proseguire:

1. 5320-0235=5085
2. 8550-0558=7992
3. 9972-2799=71737
4. 731-1377=6354
5. 6543-3456=3087
6. 8730-0378=8352
7. 8532-2358=6174
8. 7641-1467=6174

Al 7° passaggio siamo arrivati alla costante di Kaprekar, in un certo senso siamo caduti in trappola visto che, da questo momento in poi, possiamo ripetere l’operazione quante volte vogliamo ma non ci sposteremo più dal numero 6174, infatti è possibile dimostrare che:

applicando l’algoritmo di Kaprekar partendo da un qualsiasi numero di 4 cifre, di cui almeno 2 diverse tra loro, si raggiunge il numero 6174 al massimo in 7 passaggi.

Questo risultato vale anche per i numeri di 1, 2 o 3 cifre a patto di aggiungere degli zeri a sinistra in modo da renderli di 4 cifre, ad esempio per applicare l’algoritmo al numero 43 dobbiamo scriverlo nella forma 0043. Le sole eccezioni si hanno per i numeri composti da 4 cifre uguali (es. 3333) poiché in questi casi la procedura porterà subito al numero 0 (3333-3333=0) che è anche esso costante (0000-0000=0000).

Ma è una cosa che funziona solo con i numeri di 4 cifre? In effetti no, esiste anche una costante di Kaprekar per i numeri di 3 cifre, si tratta del numero 495, infatti se calcoliamo 954-495 otteniamo proprio 495.

Per i numeri a 6 cifre ne esistono addirittura due di numeri che tornano su se stessi, 631764 e  549945. Tuttavia in molti casi, come per i numeri a 1, 2, 5 o 7 cifre, non esistono costanti di Kaprekar, ma al massimo dei cicli, ovvero delle sequenze di numeri che si susseguono uno dopo l’altro ciclicamente.

Ma come facciamo ad essere sicuri che solo 6174 e 495 (e le altre costanti di Kaprekar) tornano su se stessi? In effetti non c'è niente di misterioso, non si tratta di magia, e lo si può dimostrare con un ragionamento, basato sul funzionamento della sottrazione in colonna, che però è piuttosto elaborato. In alternativa possiamo possiamo usare la forza bruta e provare ad applicare l'algoritmo a tutti i numeri composti da una data quantità di cifre. Quest’ultima strategia è fattibile soprattutto quando si dispone di un computer e si ha a che fare con numeri relativamente piccoli. Essa permette di raccogliere tutti i dati sul numero dei passaggi che servono, di volta in volta, per cadere in trappola in una costante di Kaprekar, dati che possono essere rappresentati graficamente, come nella figura sotto.

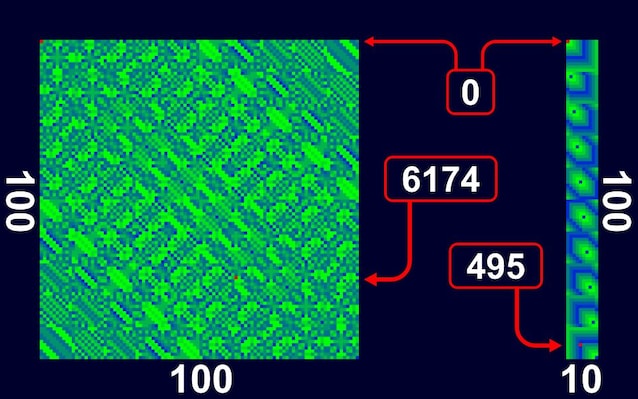
Questa rappresentazione grafica dimostra che 6174 e 495 sono le uniche costanti di Kaprekar (non nulle) per i numeri di 4 cifre e di 3 cifre. Il grande quadrato sulla sinistra, di lato 100×100 si riferisce a tutti i numeri di 4 cifre, disposti in file da 100, dove il primo quadratino in alto a sinistra corrisponde al numero zero ed è rosso perché con l'algoritmo di Kaprekar lo zero torna su se stesso, l'altro puntino rosso corrisponde proprio al numero 6174. Laddove i quadratini sono di color blu intenso significa che l'algoritmo richiede il numero massimo di passaggi prima di terminare nella costante di Kaprekar, mentre se il colore è verde intenso è richiesto 1 solo passaggio, i colori intermedi rappresentano le situazioni intermedie. Analogamente la banda verticale sulla destra della figura rappresenta il caso dei 1000 numeri di tre cifre, disposti in 100 file da 10. In entrambi i casi le figure mostrano evidenti regolarità che vanno a formare piacevoli motivi grafici … almeno dal punto di vista di un matematico!

non perderti questo video

Il quadrato magico, tra magia e matematica: tipologie e come costruirli