
Nell'indovinello delle pillole la situazione è questa: ogni mattina devi prendere due pillole, una rossa e una blu, che tieni in due scatole distinte. Una mattina quindi, come tutte le mattine, ti prepari per prendere le tue due medicine, ma salta la luce e la stanza rimane completamente al buio (esiste anche la versione dell'indovinello in cui non salta la luce, bensì chi deve prendere le pillole è cieco, ma il quesito rimane lo stesso).
Succede però un imprevisto: le due pillole ti cadono per terra. Per questo, decidi di prenderne altre due, una per ogni scatola, così da essere sicuro di avere in mano una pillola rossa e una pillola blu. Ma purtroppo… ti cadono di nuovo! Ma non solo, le pillole dentro le scatole sono finite. Quindi ti ritrovi con quattro pillole per terra, due rosse e due blu, che non riesci a distinguere tra loro, di cui devi riuscire a prenderne esattamente una rossa e una blu. Come fare?
La soluzione all'indovinello della pillola rossa e blu
Il primo pensiero che viene alla mente è ragionare in senso probabilistico, pensando a quale sia la probabilità di pescare esattamente una pillola blu e una rossa da un gruppo di quattro pillole, di cui due rosse e due blu. Tralasciando i conti probabilistici, non esiste alcun caso in cui si possa avere certezza di aver pescato proprio una pillola rossa e una blu!
E quindi, come fare? La risposta sta nel… dividerle! Se raccogliamo tutte e quattro le pillole, le mettiamo in fila e le tagliamo tutte quante a metà, scegliendo tutte le metà superiori – oppure tutte le metà inferiori – saremo sicuri di avere esattamente due metà blu e due metà rosse, e quindi esattamente una pillola blu e una pillola rossa, e senza bisogno dell'aiuto della luce (o della vista)!
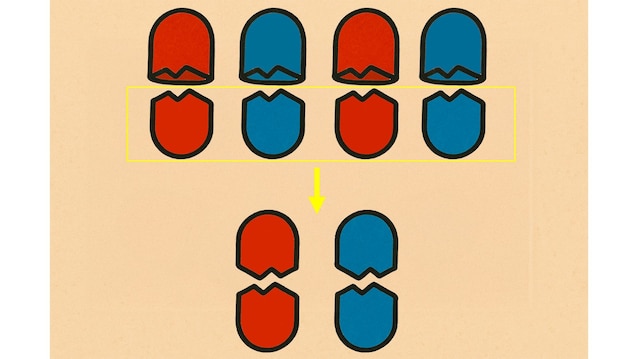
;Resize,width=767;)


;Resize,width=578;)
;Resize,width=767;)

;Resize,width=727;)
;Resize,width=727;)
;Resize,width=727;)
;Resize,width=727;)

