Perché i numeri alla seconda sono detti quadrati perfetti? Cosa sono i numeri figurati

Sembra banale ma.. come mai i numeri elevati alla seconda – come ad esempio 4, che è 2² – vengono detti quadrati (o quadrati perfetti quando si tratta di numeri interi)? La risposta va cercata nella "forma" di questi oggetti. I numeri infatti possono essere rappresentati graficamente e nel caso dei numeri naturali, per esempio, possiamo utilizzare dei punti: • è 1, •• è 2, ••• è 3 e così via. Ecco, i numeri quadrati si chiamano così proprio perché possono essere disegnati come dei quadrati di lato uguale alla propria radice! E questi quadrati sono detti quadrati perfetti quando sono l'elevamento al quadrato di un numero intero.

E non esistono solo i numeri quadrati, ma anche rettangolari, triangolari e perfino esagonali!
Lo vediamo in questo articolo, insieme ad alcune curiosità numeriche che i numeri figurati ci riescono a mostrare… disegnando!

Come mai i numeri alla seconda vengono detti quadrati?

A molti potrà sembrare una domanda banale, ma sono in molti a non saper trovare una risposta su due piedi: perché i numeri elevati alla seconda vengono detti quadrati? Ebbene sì, c'entra proprio la forma del quadrato e adesso capiremo il perché. Prima di tutto ricordiamo che qualsiasi numero se elevato alla seconda viene detto quadrato, mentre i quadrati perfetti sono l'elevamento alla seconda dei soli numeri interi, cioè di quei numeri che non presentano la virgola.

I numeri ci aiutano a contare gli oggetti, infatti sono qualcosa di astratto, dei simboli che indicano proprio la quantità di elementi che vogliamo contare Il fatto che indichino una quantità, però, ci suggerisce che i numeri stessi possano essere rappresentati attraverso degli oggetti, come per esempio dei punti! È proprio così che li abbiamo imparati quando andavamo alle elementari.

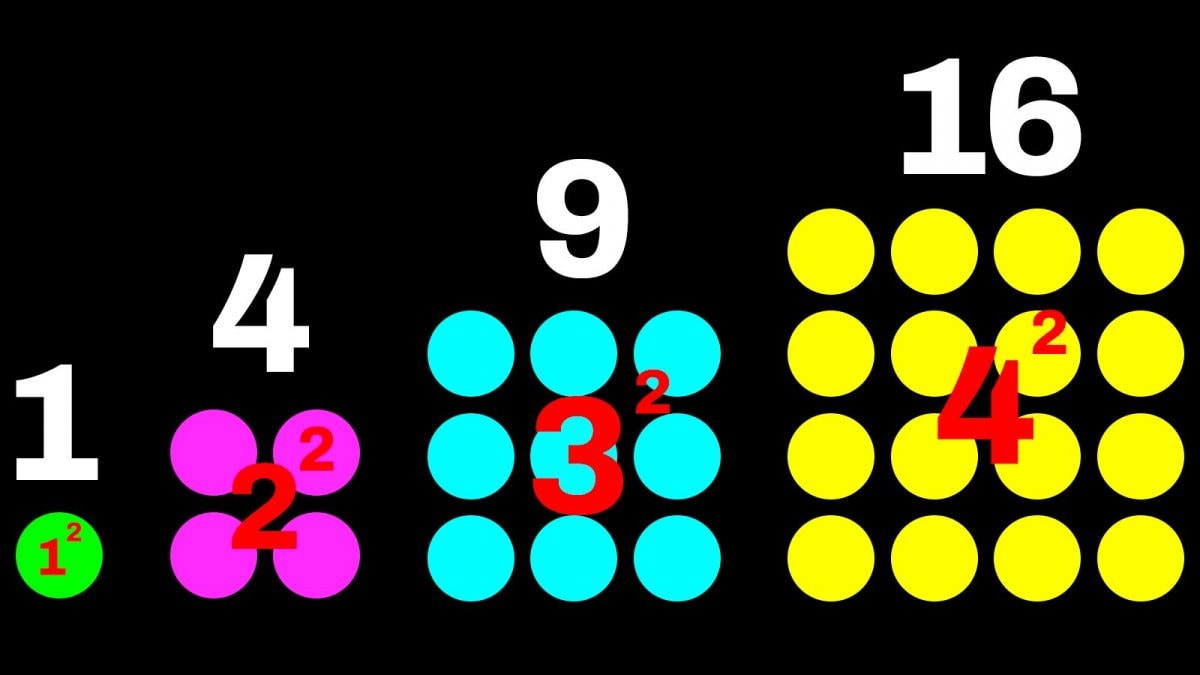
Ecco, se proviamo a disegnare i numeri alla seconda con dei puntini – cioè i numeri quadrati – ci accorgeremo che sono proprio.. dei quadrati! Ogni quadrato perfetto infatti, cioè un quadrato ottenuto elevando alla seconda un numero intero, può essere disegnato come un insieme di punti equidistanti disposti a formare un quadrato geometrico con lato uguale alla propria radice. Per esempio, 4 (2²) è un quadrato di lato 2, 9 (3²) è un quadrato di lato 3, 16 (4²) è un quadrato di lato 4 e così via.

Non solo quadrati: cosa sono i numeri triangolari e rettangolari

Quelli che abbiamo visto sono i cosiddetti numeri figurati, cioè numeri naturali che possono essere rappresentati tramite uno schema geometrico regolare di punti. E non esistono solo i quadrati! Ma anche i triangoli, i rettangoli, perfino gli esagoni!

Tutti i numeri naturali sono rettangoli

Per quanto riguarda i rettangoli, va detto che qualsiasi numero naturale n può essere rappresentato come un rettangolo di lati uguali a 1 e n. Ci sono numeri che però possono essere rappresentati come rettangoli in più modi diversi: dipende infatti dal proprio numero di divisori. Se prendiamo per esempio il numero 6, può essere rappresentato come una fila di 6 punti oppure 2 file da tre punti. E possiamo anche notare che un numero può avere più figurazioni: il quattro, per esempio, è sia rettangolare (1×4) che quadrato (2×2).

I numeri quadrati sono somme di numeri triangolari consecutivi

Poi ci sono i numeri triangolari che, come si vede nella figura sotto, possono essere ottenuti disponendo in modo regolare i punti a formare una "piramide". Possiamo notare che i numeri triangolari si ottengono sommando in successione i numeri naturali partendo dall'1: 1, 3 (1+2), 6 (1+2+3), 10 (1+2+3+4) e così via.

C'è una particolarità che rende affascinanti i numeri triangolari: quando sommiamo due numeri triangolari consecutivi, otteniamo sempre un numero quadrato. Per esempio, se sommiamo 10 e 15, otteniamo 25 che è proprio 5 alla seconda. Questa proprietà può essere intuita graficamente, come vediamo nella figura sotto.

I numeri figurati aiutano a scoprire verità matematiche

Disegnare i numeri non è un semplice divertimento, ma ci aiuta anche a scoprire interessanti intuizioni matematiche. Per esempio, se disegniamo i numeri dispari uno di fianco all'altro come rettangoli, possiamo facilmente notare che sommando i numeri dispari consecutivi a partire dall'1, otteniamo sempre un numero quadrato come possiamo vedere nella figura sotto. Ed è vero!

La somma dei primi n numeri dispari è sempre uguale a un quadrato, e nello specifico è uguale proprio a n².

non perderti questo video

Perché i numeri hanno la forma che hanno e li scriviamo così? A proposito: non sono arabi