Se un tavolino traballa, basta ruotarlo: cos’è il teorema dei valori intermedi al bar

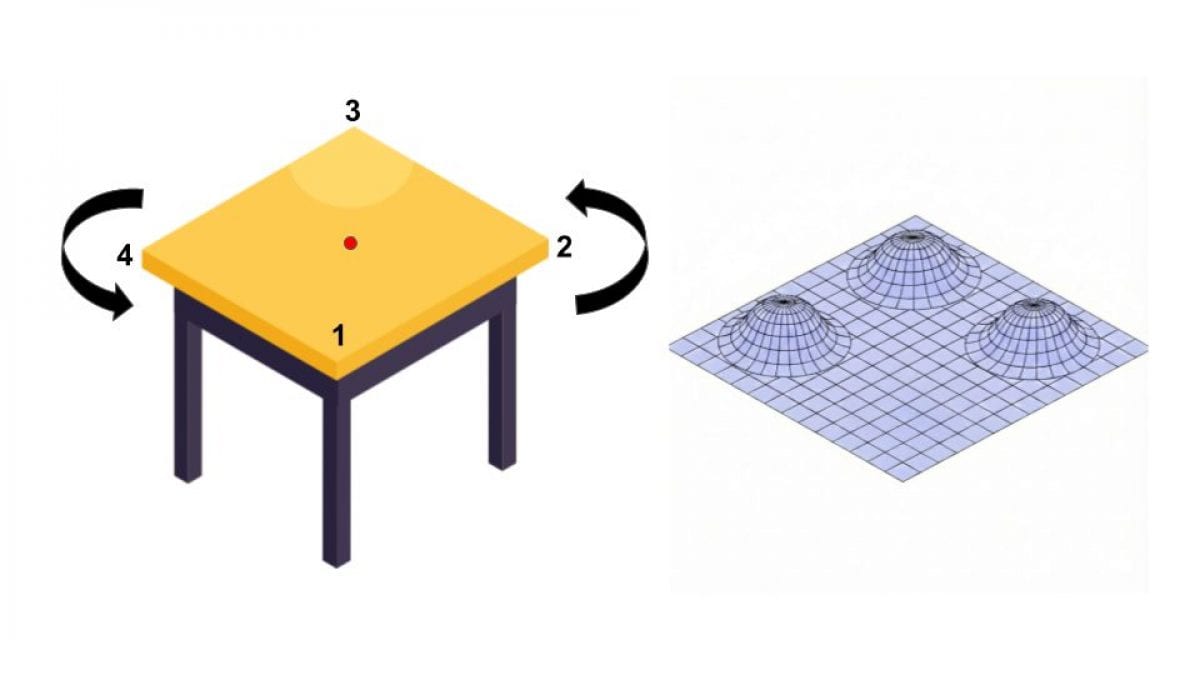
Se ci troviamo nel dehor di un bar e il nostro tavolino è traballante, una possibile soluzione è quella di prendere un pezzo di carta, ripiegarlo e infilarlo sotto una delle gambe. Questa soluzione, però, non è definitiva: dopo un po’ di tempo, la carta si comprimerà e il tavolino tornerà a traballare. Possiamo allora tentare una soluzione più elegante e matematica: ruotare il tavolo. Sembra incredibile, ma se abbiamo un tavolino quadrato con quattro gambe posizionato su un pavimento irregolare (ma non troppo), la matematica ci garantisce che ruotando di poco il tavolo riusciremo a trovare una posizione in cui tutte e quattro le gambe appoggiano per terra, rendendo così il tavolo stabile.

Vediamo meglio come fare e qual è il teorema da cui dipende questa proprietà.

Perché il tavolo traballa

Un tavolo con quattro gambe uguali, in teoria, è stabile. Ma questo vale solo se il pavimento è perfettamente piano. Nella realtà, spesso capita di trovarsi su superfici irregolari: un selciato, una terrazza, il pavé di una piazza. In questi casi, tre gambe del tavolo possono appoggiarsi a terra, ma una rimane sollevata, causando l’instabilità.

A porsi seriamente il problema di come evitare che il suo tavolino traballasse è stato, tra gli altri, André Martin, fisico del CERN. Martin ha lavorato a lungo sulla fisica delle particelle ma amava anche ragionare su argomenti più leggeri (come la stabilità dei tavolini). Aveva notato che i tavolini sulla terrazza della mensa del CERN, per quanto fossero perfettamente interi, spesso traballavano a causa del terreno irregolare. Studiando il problema dal punto di vista matematico, Martin dimostrò che, se il terreno non presenta pendenze esagerate (superiori a 15 gradi), esiste sempre un angolo di rotazione in cui tutte e quattro le gambe toccano il suolo. E funziona anche nella pratica: Martin racconta di averlo testato personalmente molte volte, ruotando i tavoli della terrazza finché non trovava la posizione giusta.

Come ruotare il tavolino nel modo giusto

Come abbiamo detto, il tavolino è stabile solo se tutte e quattro le gambe toccano contemporaneamente a terra. Se ci troviamo davanti un tavolino instabile, quindi, dobbiamo appoggiarci una mano sopra per fare in modo che tre delle quattro gambe tocchino terra e restino aderenti al suolo e poi ruotare lentamente il tavolo, finché anche la quarta troverà il suo punto d’appoggio.

Durante questa rotazione è importante cercare di mantenere fermo il centro del tavolo (indicato dal pallino rosso nella figura), così da non cambiare l'assetto delle tre gambe già a contatto. Non importa in quale direzione lo si ruota, e non serve girare molto: bastano al massimo 90 gradi. Se il terreno non è eccessivamente irregolare, la matematica ci garantisce che esiste almeno una posizione in cui il tavolo smetterà di traballare.

Attenzione però: questo non significa che il piano sarà perfettamente orizzontale o “in bolla”, ma semplicemente che non si muoverà più quando ci appoggiamo sopra qualcosa.

Perché funziona: la spiegazione

Per capire la matematica dietro questo trucco, immaginiamoci un terreno con tre gobbe rialzate, su cui poggiano le gambe 2, 3 e 4 e una parte in piano, sopra cui è sospesa la gamba 1. Il nostro tavolo, in questo momento, è completamente orizzontale, ma è anche del tutto instabile: se ci appoggiamo qualcosa sopra, crollerà tutto.

Ora ruotiamo lentamente il tavolo di 90 gradi, facendo perno sul centro e mantenendo le gambe 2, 3 e 4 fermamente incollate al terreno. Durante la rotazione:

• La gamba 2, che inizia dalla gobba in basso a destra, scende fino al piano e poi risale.
• La gamba 3, che inizia dalla gobba in alto, fa lo stesso.
• La gamba 4, che inizia dalla gobba in basso a sinistra, scende e si ferma sul piano, più in basso rispetto a dove era partita.
• La gamba 1, quella inizialmente sospesa, si abbassa seguendo il movimento delle altre durante la rotazione e ruotando incontra la gobba sulla destra. A questo punto, per continuare a ruotare, vorrebbe poter risalire, ma non può farlo: la gamba 4, infatti, si trova già appoggiata su una zona più bassa, e il tavolo (essendo rigido) non può piegarsi o deformarsi per permettere alla gamba 1 di salire. Per poter continuare la rotazione fino ai 90 gradi, quindi, la gamba 1 deve scavare un buco all’interno della gobba e infilarsi sotto il livello del terreno.

Fermiamoci un attimo a osservare come si è mossa la gamba 1 mentre facevamo ruotare il tavolo. All’inizio si trovava sopra il livello del terreno, senza toccarlo: la distanza tra la gamba e il suolo era quindi positiva. Alla fine della rotazione, invece, la gamba si troverebbe sotto il livello del terreno: in quel caso la distanza sarebbe negativa.

Naturalmente, il nostro obiettivo non è far sprofondare la gamba nel terreno, ma trovare il momento in cui tutte e quattro le gambe sono appoggiate a terra. In altre parole, cerchiamo l’istante in cui la distanza tra la gamba 1 e il terreno è esattamente zero.

Se rappresentiamo questa distanza con un grafico mentre il tavolo ruota, otteniamo una curva che parte da un valore positivo e arriva a un valore negativo, più o meno così:

Come mostra il grafico, c’è necessariamente un punto in cui la distanza diventa zero. Questo non è un caso: è una conseguenza diretta di un famoso risultato matematico, il teorema dei valori intermedi. Il teorema afferma che:

Se una funzione continua assume un valore positivo in un punto e un valore negativo in un altro, allora da qualche parte tra i due deve valere zero.

Applicato al nostro problema, questo significa che, ruotando un tavolino quadrato e mantenendo tre gambe sempre a contatto con il terreno, esiste sicuramente una posizione in cui anche la distanza tra la quarta gamba e il terreno sarà zero e toccherà il suolo. In quel momento il tavolo sarà stabile, provare per credere.

non perderti questo video

Una scimmia instancabile che schiaccia tasti a caso può veramente scrivere la Divina Commedia?