Fogli A3, A4 e A5: cosa cambia e perché hanno queste dimensioni?

I fogli che usiamo comunemente hanno un formato preciso, l'A4, che ha dimensioni di 21 cm x 29,7 cm. Questa misura può sembrare casuale o poco intuitiva, ma nasconde in realtà una proprietà geometrica specifica: piegando un foglio A4 in due metà lungo il lato maggiore, si ottengono due fogli che hanno area dimezzata ma mantengono perfettamente le proporzioni del foglio di partenza. La proporzione di un foglio A4 è l'unica con questa proprietà. Questa proporzione viene mantenuta anche se raddoppiamo un foglio A4 affiancandolo a un altro: si ottiene un foglio avente il doppio dell'area, ma che mantiene perfettamente le proporzioni del foglio A4 di partenza. Quelli che abbiamo appena descritto sono proprio i formati A5 e A3, rispettivamente metà e doppio dell'A4.

Questo tipo di formati è stato definito nel 1922 partendo dal foglio A0, mantenendo le proporzioni.
Ma com'è geometricamente possibile? Lo vediamo in questo articolo.

Lo standard internazionale ISO 216: formati diversi ma proporzionalmente uguali

Il formato di carta più utilizzato è sicuramente l'A4, che ha come dimensioni 21 cm x 29,7 cm, fa parte di una specifica serie di formati di carta – la serie A – stabilita dall'Organizzazione Internazionale per la normazione in modo da definire norme tecniche comuni a livello mondiale.

non perderti questo articolo

Calcestruzzi fibrorinforzati, cosa sono, a cosa servono e cosa cambia rispetto all’Eternit

Lo standard per i fogli, denominato ISO 126, è stato stabilito a partire da una convenzione adottata in Germania nel 1922 dal Deutsches Institut für Normung e partiva dal foglio A0, un foglio di 1 m² la cui dimensione dei lati (841 mm x 1189 mm) fu stabilita in modo che il loro rapporto fosse uguale a √2.

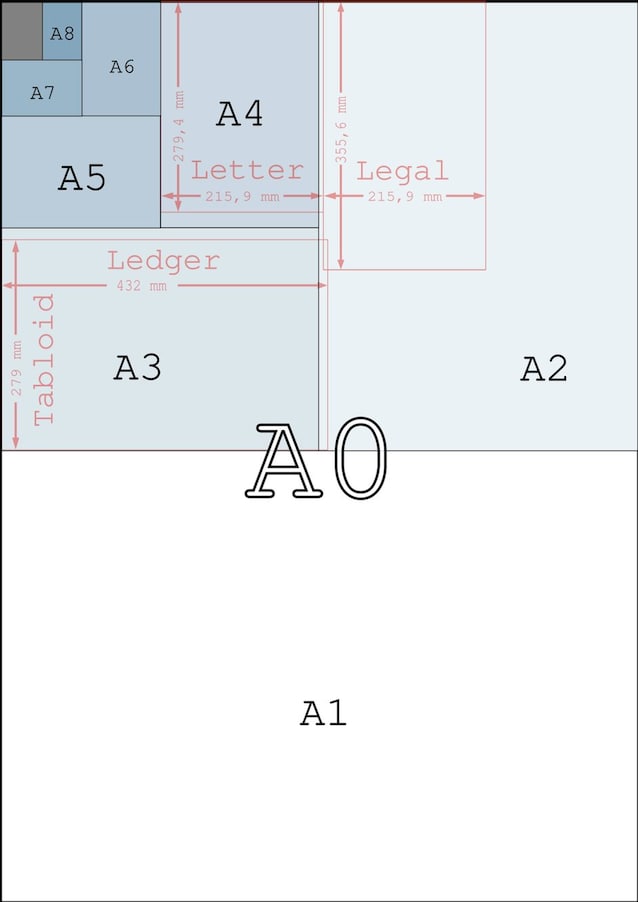
Si può dimostrare che questa specifica proporzione tra i lati (1 : √2) fa sì che dimezzando il foglio lungo il lato maggiore, si ottengano due fogli aventi metà dell'area ma che mantengono le stesse identiche proporzioni del foglio di partenza.
In questo modo, partendo dall'A0, si ottengono i formati A1, A2, A3, A4, A5 e così via, aventi area dimezzata di formato in formato, ma che mantengono le stesse proporzioni. Facendo infatti il rapporto tra le dimensioni dei lati di un foglio A4 si ottiene 29,7/21 ≃ 1,4142 ≃ √2, e lo stesso accade calcolando il rapporto tra i lati degli altri formati.

Il fatto che passando di formato in formato venga mantenuta la proporzione tra i lati ha un risvolto estremamente pratico: consente di mantenere le immagini perfettamente proporzionate se passate da un formato all'altro. Questo è il motivo per cui, per esempio, nelle stampanti possiamo scegliere se stampare in A3, A4 oppure con foglio doppio sopra il formato A4, e cioè in A5: qualunque sia il formato scelto, siamo certi che ciò che stamperemo non verrà deformato.

Ma come mai questo specifico valore del rapporto, √2, garantisce che le proporzioni vengano mantenute dimezzando un formato?

Il rapporto √2 permette di mantenere la proporzione tra un formato e l'altro

Per capire come mai un rettangolo – cioè un foglio – che ha rapporto tra i lati uguale a √2, mantiene le proporzioni se dimezzato, consideriamo un rettangolo qualsiasi e chiamiamo i suoi lati A e B. Le dimensioni di A e B sono tali che il loro rapporto A/B è uguale proprio a √2.

Adesso dimezziamo il foglio lungo il lato maggiore, ottenendo così due rettangoli che hanno aria uguale alla metà di quello di partenza, e lati uguali a B e A/2. Se calcoliamo adesso il rapporto tra i due lati, otteniamo:

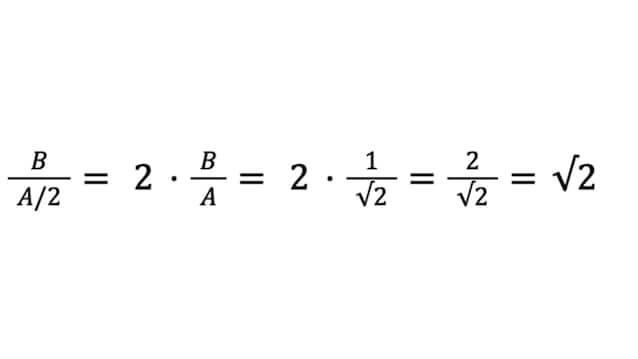
Dunque, dimezzando il foglio, la proporzione tra i lati viene mantenuta, e questo accade per qualsiasi valore di A e B tali che il loro rapporto sia √2.