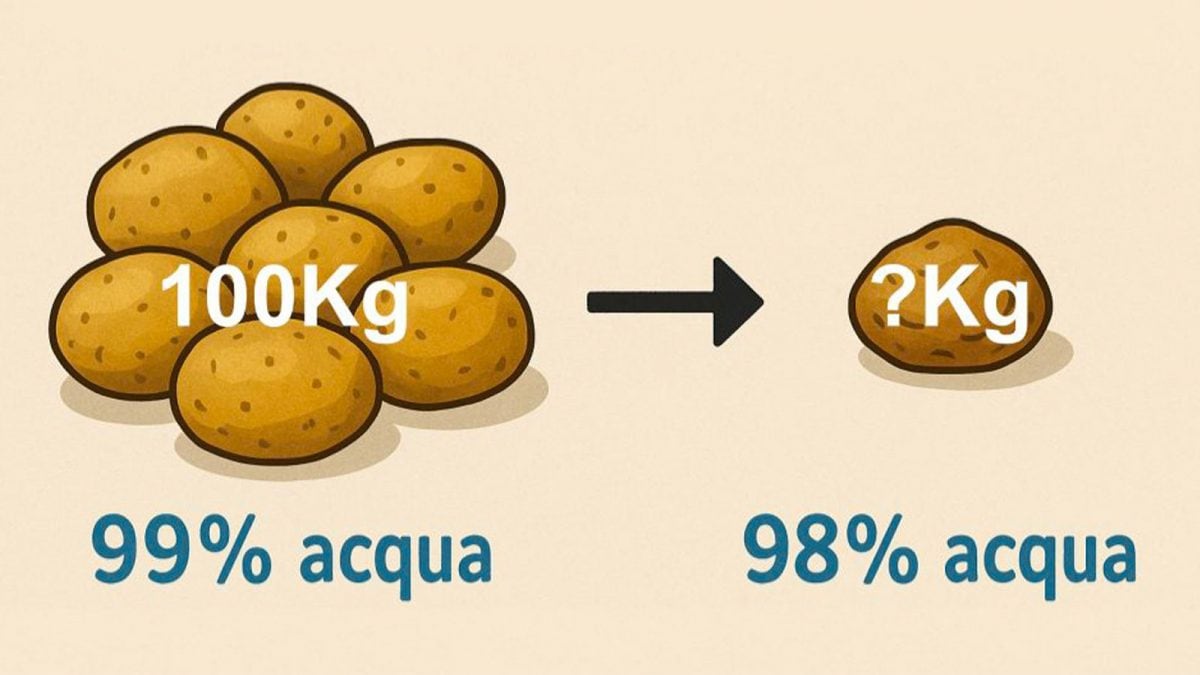
Il “paradosso della patata” è il dilemma matematico che mette alla prova l’intuito: la soluzione

Il paradosso della patata è un enigma matematico che mette in crisi la nostra capacità di interpretare le percentuali. La situazione è questa: ci sono 100 kg di patate composte al 99% di acqua che vengono lasciate essiccare fino a far scendere la percentuale di acqua al 98%. Quanti chili pesano adesso le patate? Questa domanda apparentemente semplicissima, si porta dietro un indovinello tutt'altro che banale. Vediamo la sorprendente soluzione di questo dilemma, perché può essere chiamato paradosso, e vediamo una possibile applicazione ad un contesto economico.

Cos'è il paradosso della patata

La situazione è questa: abbiamo 100 kg di patate, che sono composte al 99% di acqua, e le lasciamo essiccare. Dopo un po’ di tempo la percentuale d’acqua è scesa al 98% e le patate, che contengono un po’ meno acqua di prima, pesano un po’ meno di 100 kg, ma quanto pesano esattamente?

Questo dilemma, apparentemente facile, ha una soluzione sorprendente. Se avete pensato che alla fine le patate pesino 99 kg, di cui 98 kg di acqua… avete sbagliato! Ma non preoccupatevi, è una risposta comune, seppur erronea.

La chiave per risolvere il problema è di concentrarsi sulla parte secca invece che sull'acqua. All’inizio, quando l’acqua costituisce il 99% delle patate, la parte secca corrisponde al rimanente 1% dei totali 100 kg di patate, quindi pesa esattamente 1 kg: abbiamo 99 kg di acqua ed 1 kg di parte secca. Durante il processo di essiccazione le patate perdono solo acqua, quindi la parte secca non diminuisce e continua a pesare 1 kg. Una volta terminato il processo di essiccazione, se l’acqua costituisce il 98% delle patate, allora la parte secca corrisponde al rimanente 2% del totale, ma continua a pesare 1 kg. E quindi, qual è la soluzione?

La soluzione al paradosso matematico

A questo punto possiamo arrivare alla soluzione tramite una proporzione. Considerato che 1 kg di patate corrisponde al 2% del totale possiamo scrivere la proporzione

2% : 100% = 1 kg : totale kg

ovvero

la parte in percentuale (2%) sta al totale in percentuale (100%) come la parte in kg (1 kg) sta al totale in Kg.

Si possono scrivere diverse proporzioni equivalenti, ma tutte daranno come soluzione il calcolo

Totale kg = (1 kg × 100%) ÷ 2% = 100 kg ÷ 2 = 50 kg

quindi, il peso totale delle patate si è dimezzato, come possiamo anche vedere in maniera intuitiva dall'immagine qui sotto.

Perché lo chiamiamo paradosso e come possiamo applicarlo ad altre situazioni

In realtà non si tratta di un vero e proprio paradosso, ma di un problema apparentemente banale che ha una soluzione sorprendente, molto diversa da quello che ci aspetteremmo a prima vista. Problemi come questo ci mettono in guardia sulle difficoltà ed i risultati inaspettati in cui possiamo imbatterci quando abbiamo a che fare con proporzioni e percentuali, due concetti matematici con i quali in molti si sentono a proprio agio ma che a volte riservano delle sorprese sgradite.

Ma in che modo possiamo applicare questo paradosso ad altri contesti? Possiamo farlo in tutte quelle situazioni in cui ci sono un totale composto da parti suddivise in percentuali diverse e in cui, in seguito a qualche evento, cambiano le percentuali di composizione del totale. Ad esempio, supponiamo di avere 1000 € di cui il 99% in criptovaluta (come i Bitcoin), e supponiamo che a seguito di un calo del valore della criptovaluta la percentuale dei Bitcoin nel mio capitale cali da 99% a 98%: quanti soldi abbiamo alla fine? Applicando il ragionamento visto sopra sappiamo che un calo dal 99% al 98% corrisponde a un dimezzamento del totale, quindi il nostro capitale sarà passato da 1000 € a 500 €, una differenza non da poco.

non perderti questo articolo

Il paradosso di Simpson: quando i dati possono ingannare e come evitarlo