Il problema dei 7 ponti e la nascita della teoria dei grafi

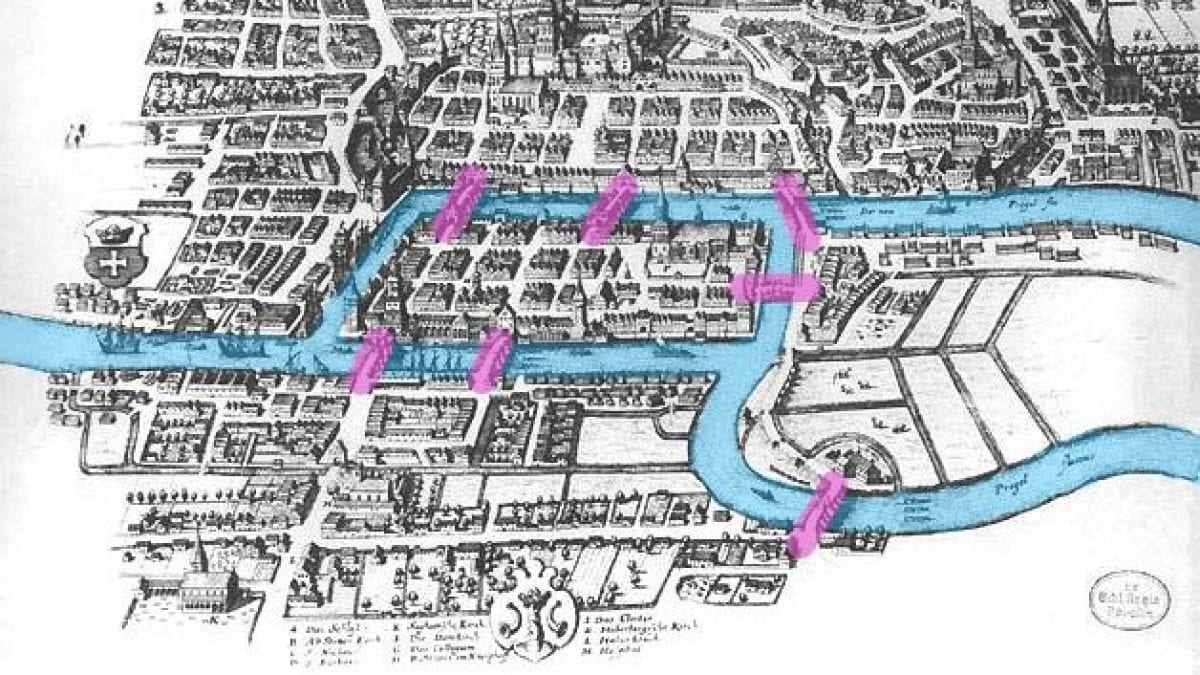
La città prussiana di Königsberg (oggi Kaliningrad in Russia) era attraversata dal fiume Pregel e collegata da sette ponti che univano tra loro due isole e le sponde opposte, dividendo la città in quattro zone.  La leggenda narra che tra gli abitanti circolava un passatempo curioso: trovare un percorso che attraversasse tutti i ponti una sola volta. Un'idea semplice, ma nessuno sembrava riuscire nell’impresa.

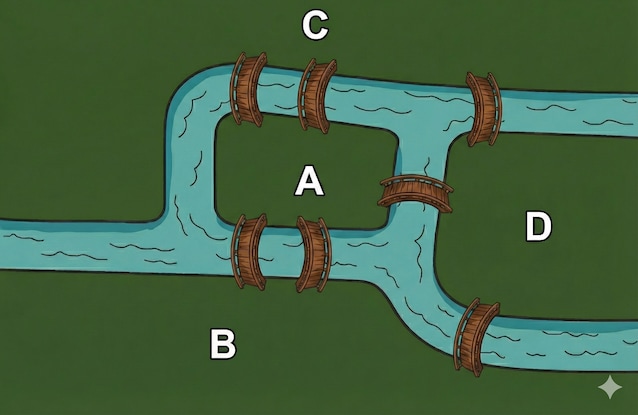
La questione finì nelle mani del matematico Leonhard Euler (in italiano noto come Eulero). All’inizio Eulero non era convinto che si trattasse di un vero problema matematico, ma osservando la mappa della città ebbe un’intuizione decisiva: non contava come ci si muoveva sulle quattro zone della città (in figura A,B,C e D,), ma solo l’ordine in cui si attraversavano i ponti.

Da qui la semplificazione brillante: rappresentare le porzioni di terra come punti e i ponti come linee.

E quindi il problema poteva essere schematizzato così:

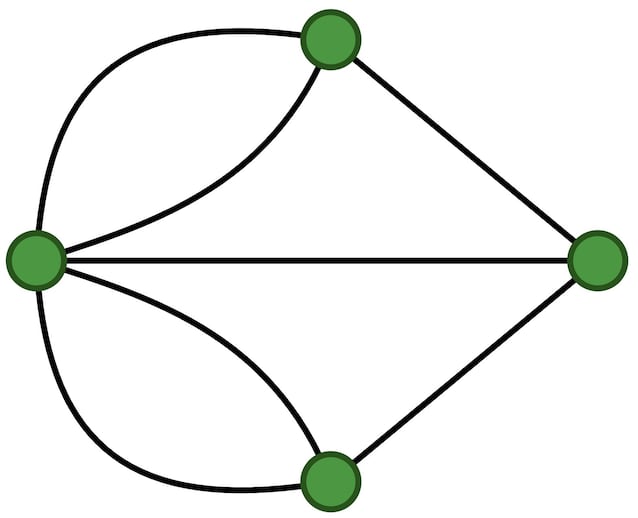
Senza rendersene conto, Eulero stava inventando la base di una nuova disciplina, la teoria dei grafi, tutt’oggi fondamentale per studiare schemi che possono essere ridotti a elementi e collegamenti.

Un grafo è un modo semplice per rappresentare collegamenti: è formato da punti (chiamati nodi) e linee che uniscono quei punti (chiamate archi).
Analizzando il sistema, scoprì che la possibilità di attraversare tutti i ponti una sola volta dipende esclusivamente dal numero di linee che “toccano” ogni punto, cioè dal grado dei nodi. Un percorso del genere – oggi chiamato cammino euleriano – è possibile solo se:

• tutti i nodi hanno un grado pari (cioè un numero pari di linee collegate al punto),

oppure

• esattamente due nodi hanno grado dispari (punto di partenza e di arrivo).

Il problema? A Königsberg tutti e quattro i nodi erano di grado dispari. In altre parole, la sfida cittadina era impossibile già in partenza.

Ironia della sorte, l’unico modo per rendere il rompicapo risolvibile sarebbe stato eliminare almeno uno dei ponti. Cosa che avvenne davvero, ma in modo tragico: durante la Seconda guerra mondiale, parte della città e alcuni ponti furono distrutti dai bombardamenti, prima che Königsberg venisse trasformata nell’attuale Kaliningrad.

La soluzione di Eulero, però, è sopravvissuta molto più dei ponti originali. Quel semplice rompicapo urbano ha dato il via alla teoria dei grafi e, più in generale, a un nuovo modo di ragionare sulle forme e sui collegamenti, aprendo la strada alla moderna topologia.

non perderti questo video

Tutto è connesso: a cosa serve la teoria dei grafi e perché è la chiave per capire i sistemi complessi