La sezione aurea è il numero più irrazionale di tutti: perché e cosa significa

La sezione aurea è un numero irrazionale, indicato con la lettera greca φ, che vale circa 1,618 e corrisponde al rapporto che devono avere due lunghezze per fare in modo che la lunghezza maggiore e la somma delle due lunghezze stiano nello stesso rapporto. Si trova spontaneamente in natura e spesso è associato alla bellezza estetica, ma da un punto di vista puramente matematico è speciale perché è considerato il più irrazionale di tutti i numeri irrazionali. matematici indicano con la lettera greca φ, e che risponde alla seguente domanda di tipo geometrico

Se dobbiamo suddividere un segmento lungo 1 in due parti in modo che l’intero segmento stia alla parte più grande come la parte più grande sta alla parte più piccola. Quanto dovrà essere lunga la parte grande? Ovvero quanto dovrà valere il rapporto (la divisione) tra le due parti?

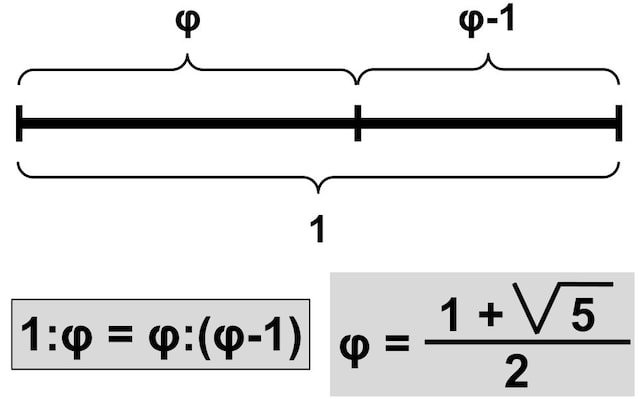
La soluzione a questo problema si trova risolvendo un’equazione di secondo grado a partire dalla proporzione "1:φ=φ:(1-φ)" ed è un numero che si calcola con frazioni e radici quadrate (vedi figura sopra). Se scriviamo questo numero in forma decimale otteniamo

φ=1,6180339887…

dove i puntini indicano che le cifre dopo la virgola sono infinite e si susseguono in maniera irregolare: si tratta infatti di un numero irrazionale che non può essere scritto con una rappresentazione decimale finita o periodica.

non perderti questo articolo

Cos’è la sezione aurea e dove si trova in natura

Cerchiamo di capire meglio,

i numeri razionali sono tutti quei numeri che possono essere scritti come frazione, con numeratore e denominatore interi, senza virgole.

Ad esempio ¾ e ⅓  sono numeri razionali mentre la sezione aurea non lo è, si dice invece che è irrazionale perché, a causa di quella radice quadrata di 5 che serve per calcolarla (vedi figura sopra),

i numeri irrazionali non possono essere scritti come frazione con numeratore e denominatore interi.

Quando proviamo a scrivere un numero razionale in forma decimale ci sono solo due possibilità:

1. il numero decimale ha una quantità finita di cifre dopo la virgola, ad esempio ¾=0.75 ha esattamente due cifre dopo la virgola
2. oppure il numero decimale è periodico, ovvero ha una o più cifre che si ripetono sempre uguali, ad esempio ⅓=0.3333… con la cifra 3 che si ripete all’infinito, per cui anche se non riusciamo a scrivere tutte le cifre, sappiamo che valgono tutte 3

Al contrario, la forma decimale di un numero irrazionale, come  la sezione aurea, presenta una quantità infinita di cifre dopo la virgola che si susseguono in maniera irregolare, senza periodi, e non è possibile conoscerle tutte: al massimo cercare di calcolare più cifre possibile, come accade per il più famoso dei numeri irrazionali, il pi greco, per il quale esiste il record delle cifre note che di quando in quando viene aggiornato.

La ricerca delle cifre che stanno dopo la virgola di un numero irrazionale può richiedere più o meno tempo e nel caso della sezione aurea questa ricerca richiede moltissimo tempo, ed è per questo che viene considerata più irrazionale di pi greco e di tutti gli altri numeri irrazionali.

Ma come si fa a cercare (e magari trovare!) le cifre di un numero irrazionale come φ? Una possibilità è quella di usare le frazioni continue, un modo particolare di rappresentare i numeri che si può utilizzare per calcolare le approssimazioni dei numeri irrazionali. Vediamo di cosa si tratta.

Un frazione continua è costituita da un numero sommato ad una frazione con numeratore 1 e denominatore che contiene a sua volta un numero sommato ad un'altra frazione il cui denominatore può contenere a sua volta un un numero sommato ad una frazione, e così via.

Nella figura sotto abbiamo riportato le frazioni continue relativi ai numeri 5/3, 3/5 e 225/157.

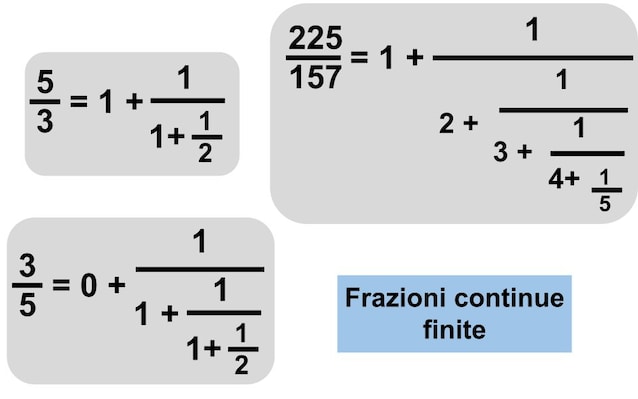
I numeri che abbiamo considerato sono tutti numeri razionali e le loro frazioni continue sono finite:

ogni numero razionale può essere rappresentato con una frazione continua finita.

Per quanto riguarda i numeri irrazionali, invece, ogni volta che ci sembra di aver trovato l’ultima frazione piccola in basso ci accorgiamo che questa contiene a sua volta una somma tra un numero ed una nuova frazione:

i numeri irrazionali non possono essere rappresentati tramite frazioni continue finite, ma solo con frazioni continue infinite.

Per quanto riguarda il caso specifico della sezione aurea la sua frazione continua contiene solo numeri uno, come si vede nella figura sotto.

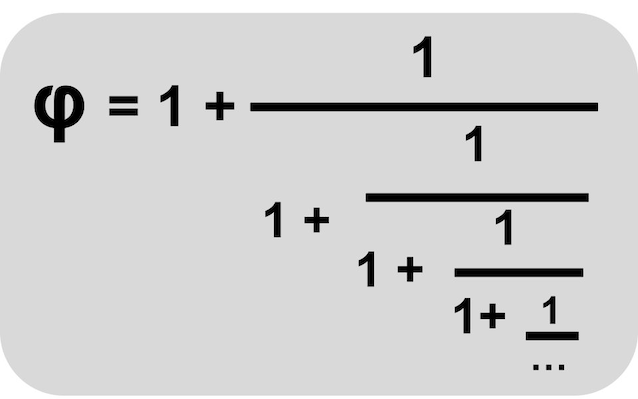
Questa frazione non è solo un modo coreografico di scrivere la sezione aurea, può anche essere utilizzata per cercarne i valori approssimati. Lo si può fare troncando la frazione continua, ovvero sostituendo con 1 la serie infinita di frazioni da un certo livello in poi. Nella figura sotto lo abbiamo fatto al terzo livello ottenendo come approssimazione il numero 3/2=1.5 che non è una gran che come approssimazione visto che solo la cifra "1" prima della virgola è uguale a quella della sezione aurea.

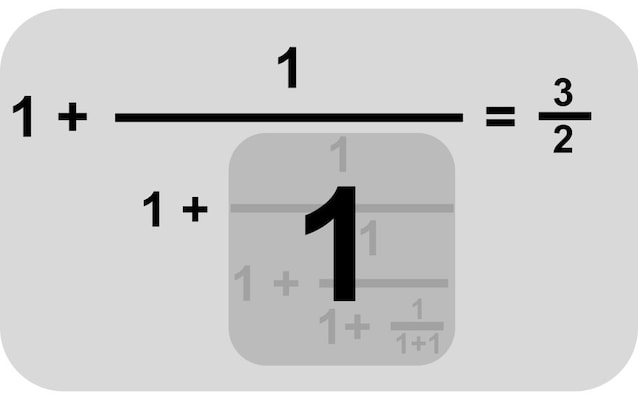
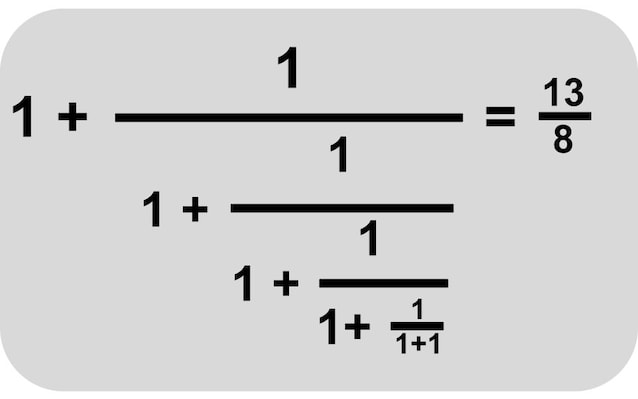
Nella figura sotto si vede come fermandosi al 6° livello l’approssimazione è 13/8 = 1,625 che condivide con la sezione aurea solo le cifre 1,6.

Utilizzando questo procedimento le prime approssimazioni di φ risultano essere nell'ordine 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, che approssimano il numero rispettivamente alle cifre 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5. Si tratta di approssimazioni che diventano sempre migliori via via che andiamo più in profondità.

Lo stesso procedimento si può usare per approssimare qualsiasi numero irrazionale a partire dalla sua frazione algebrica, ottenendo via via delle approssimazioni sempre migliori. Il problema con la sezione aurea è che questo processo di approssimazione è lentissimo, molto più lento di quello che accade per qualsiasi altro numero, ed è per questo viene considerato il numero più irrazionale di tutti, perché è talmente lontano dall’essere razionale che per approssimarlo con la sua frazione continua ci vuole un sacco di tempo, più di quello che serve per qualsiasi altro numero irrazionale.