Mangiare meno gelati fa diminuire il numero di divorzi? No: ecco la differenza tra correlazione e causalità

I dati sono uno strumento fondamentale per capire il mondo e prendere decisioni informate, ma non è sempre facile interpretarli nella maniera corretta. Per esempio, può succedere che due fenomeni si comportino nel tempo in maniera così simile da sembrare uno la causa dell'altro. Questa, però, potrebbe essere una semplice coincidenza o potrebbe dipendere da un terzo evento, che non viene osservato, e che è la causa di entrambi. Riuscire a distinguere una semplice coincidenza da un vero rapporto di causa-effetto tra gli eventi può essere complesso, ma è essenziale in campi come la sanità, la politica e l’economia, in cui vengono prese decisioni importanti basandosi sull'interpretazione dei dati. In questo articolo capiamo cosa vuol dire che due fenomeni sono "correlati",  cosa sono le correlazioni spurie e l’importanza di non confondere la correlazione (cioè una particolare relazione tra gli andamenti di due eventi) con la causalità (cioè il nesso per cui un evento è la causa dell'altro).

Fenomeni che sembrano legati tra loro, ma non lo sono

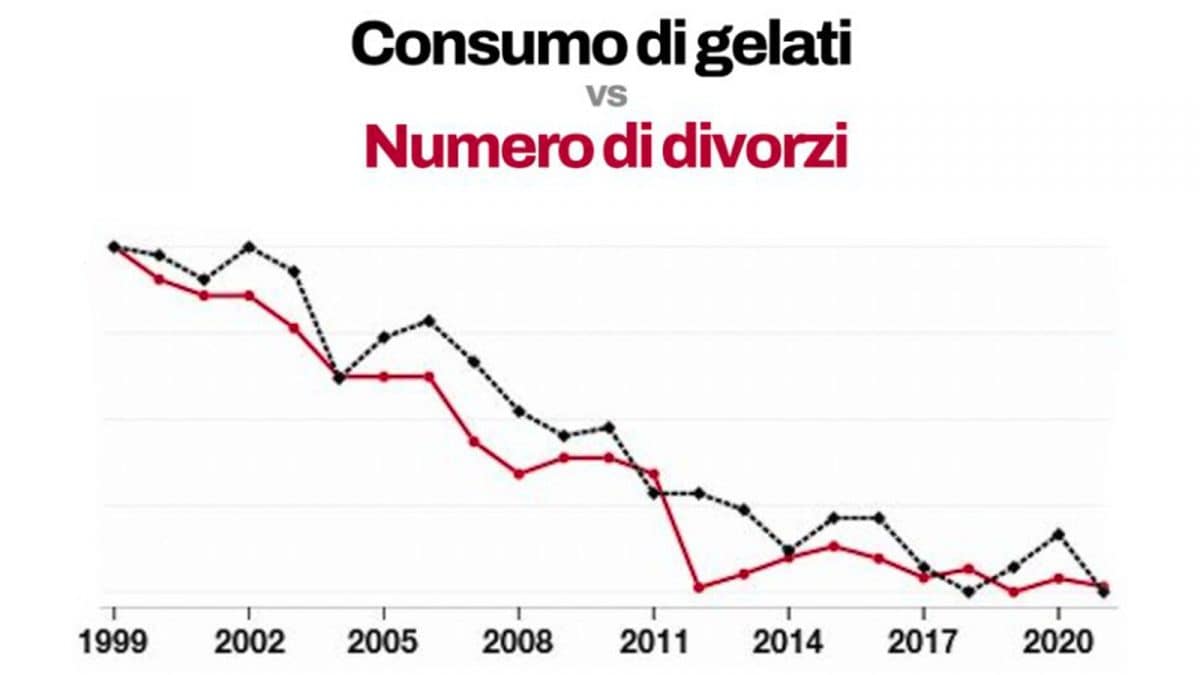
Iniziamo da un grafico e una domanda: ridurre il consumo di gelati riduce il numero di divorzi in Alabama? Ovviamente no: la quantità di gelato consumata in un anno negli Stati Uniti non influisce in nessun modo sul numero di divorzi in Alabama, ma se guardassimo solo questo grafico, potremmo pensare che sia vero.

Quello che vediamo, infatti, è che il consumo di gelato negli Stati Uniti e il numero di divorzi in Alabama sembrano diminuire in maniera analoga dal 1999 al 2020. In questo periodo, infatti, le persone hanno mangiato sempre meno gelato (da 16,2 a 12 libbre all’anno) e i divorzi sono diminuiti (da circa 6 divorzi per 1000 abitanti a 4).

Questo potrebbe quindi farci pensare erroneamente che se diminuissimo la quantità di gelato consumata, allora potremmo diminuire anche i divorzi, e questo a causa dell'estrema "somiglianza" dei due grafici. Nella lettura dei dati, è sempre importante tenere presente che situazioni del genere possono accadere per casualità, oppure – solitamente – a causa di una terza variabile che collega i due fenomeni, ma che in quel momento non stiamo tenendo in considerazione.

In statistica, quando due fenomeni variano contestualmente si dice che sono variabili correlate. Vediamo cosa significa.

Due variabili sono correlate quando cambiano insieme

Due variabili o fenomeni sono correlati quando si osserva che al variare di uno, varia anche l’altro. La correlazione descrive proprio questa tendenza di una variabile a cambiare in funzione dell'altra e si esprime con un coefficiente di correlazione che varia tra -1  e 1 in questo modo:

• 1: correlazione positiva. All'aumentare di una variabile, anche l'altra aumenta.
• -1: correlazione negativa. All'aumentare di una variabile, l'altra diminuisce.
• 0: nessuna correlazione. Le due variabili hanno andamenti totalmente indipendenti l'uno dall'altro.

Ad esempio, pensiamo al numero di ciabatte da mare vendute e al numero di persone attaccate da una medusa: entrambe le variabili aumentano durante i periodi estivi e a diminuiscono durante quelli invernali, seguendo lo stesso comportamento. Queste variabili saranno quindi fortemente correlate. Quando ci troviamo davanti a fenomeni che si evolvono nel tempo in maniera analoga o a grafici come quello dei gelati e dei divorzi, è facile pensare che non solo gli eventi siano legati tra loro, ma anche che uno dei due sia la causa dell’altro. Questa, però, è una nostra “scorciatoia mentale” e non è sempre vera.

Correlato non vuole per forza dire causativo

La correlazione tra due fenomeni, per quanto forte, non implica necessariamente che uno sia la causa dell’altro. Nel caso della vendita di ciabatte e delle punture di medusa, ad esempio, le variabili sono correlate, pur non essendo una la causa dell’altra: comprare ciabatte non ci mette a rischio di un attacco di medusa e non sentiamo l’urgenza di andare a comprare delle infradito subito dopo essere stati punti. Le ciabatte e le punture, quindi, sono correlate tra loro perché variano insieme, ma non hanno un rapporto diretto di causa-effetto.

Per dimostrare il rapporto di causalità si deve ricorrere a tecniche di inferenza causale, che puntano ad eliminare ogni fattore confondente e a lasciare come unico fattore da osservare la relazione di causa-effetto. Quando ci troviamo davanti a situazioni come quella dei gelati e dei divorzi o delle ciabatte e delle punture parliamo di correlazioni spurie.

Cosa sono le correlazioni spurie

Una correlazione spuria è la situazione in cui due o più variabili sono correlate, ma non legate da un rapporto causale. Può avvenire a causa di una coincidenza o della presenza di un terzo fattore non considerato, il "fattore confondente".

L’esempio dei divorzi e dei gelati rappresenta perfettamente la situazione in cui due variabili hanno un indice di correlazione molto alto (0.967), ma non hanno nessun legame causale. Sul sito Spurious correlation ci sono tanti altri esempi curiosi, come il rapporto tra il numero di birrifici negli Stati Uniti e l’energia solare generata in Perù (correlazione = 0.978) o il numero di lauree triennali in psicologia con il numero di giardinieri in Utah (correlazione = 0.990). Chiaramente, queste correlazioni sono solo una coincidenza.

Per quanto riguarda le punture di medusa e la vendita di ciabatte, invece, la correlazione non è una coincidenza, ma è dipendente da un fattore confondente, cioè il fattore che connette le due variabili: l’andare al mare. Entrambe le variabili, infatti, sono dipendenti da questa terza variabile: se vado al mare mi servono le infradito e più tempo passo in acqua, più è probabile che mi punga una medusa. Questa è una variabile esterna che influenza entrambi gli eventi, creando una correlazione senza una causalità diretta.

Saper distinguere tra correlazione e causalità, senza trarre conclusioni affrettate, ci può aiutare a prendere decisioni importanti in ambiti cruciali come la medicina, la politica e l’economia.