Trucchi per fare le moltiplicazioni a mente con calcoli più veloci

Esistono dei trucchi per fare le moltiplicazioni a mente, in maniera veloce, senza ricorrere alla moltiplicazione in colonna. In generale si tratta di sostituire una moltiplicazione con operazioni più semplici che diano lo stesso risultato, ma alcuni sembrano proprio dei trucchi magici. Ne vediamo alcuni, quelli che sfruttano operazioni più semplici, il trucco magico della moltiplicazione per 11 e quello del prodotto di numeri vicino a 100.

Trasformarla in operazioni più semplici

Il livello di difficoltà di un'operazione è soggettivo, ma ci sono alcune operazioni che risultano più facili e possiamo sfruttarle per fare al volo certi tipi di moltiplicazioni. Ad esempio moltiplicare per 10, per 100 o per 1000 è facilissimo, basta aggiungere uno 1, 2 o 3 zeri, ma anche raddoppiare o dimezzare è abbastanza facile: combinando queste operazioni possiamo facilmente moltiplicare per 5, 4 e per 25.

• Per moltiplicare per 5 basta moltiplicare per 10 e poi dimezzare: per calcolare 23 × 5, moltiplichiamo per 10, cioè aggiungiamo uno zero a 23 ottenendo 230, e poi dimezziamo: 230 : 2 = 115 che è proprio il risultato di 23 × 5. Questo trucco funziona perché 10 è il doppio di 5.
• Per moltiplicare per 25 basta moltiplicare per 100 e poi dimezzare due volte: per calcolare 23 × 25, moltiplichiamo per 100, cioè aggiungiamo due zeri ottenendo 2300 e poi dimezziamo due volte il numero ottenuto: calcoliamo prima 2300 : 2= 1150 e poi 1150 : 2=575 che è proprio il risultato di 23 × 25. Questo trucco funziona perché 100 è il quadruplo di 25 e dimezzare 2 volte è la stessa cosa che dividere per 4.
• Per moltiplicare per 9 basta aggiungere uno zero e poi togliere il numero che stiamo moltiplicando: per calcolare 18 × 9, moltiplichiamo per 10, cioè aggiungiamo uno zero al 18 ottenendo 180 e poi sottraiamo 18 ottenendo 180 – 18 = 162 che è proprio 18 × 9. Il trucco funziona perché 18 × 9 = 18 × (10 – 1) che per la proprietà distributiva è uguale a 18 × 10 – 118 × 1 = 180 – 18 = 162.
• Per moltiplicare un numero per 11 basta aggiungere uno zero e poi sommare il numero che stiamo moltiplicando: per calcolare 18 × 11, moltiplichiamo per 10, cioè aggiungiamo uno zero al 18 ottenendo 180 e poi sommiamo 18 ottenendo 178 che è proprio 18 × 11. Il trucco funziona perché 18 × 9 = 18 × (10 + 1) che per la proprietà distributiva è uguale a 18 × 10 + 118 × 1 = 180 + 18 = 188.

Il trucco che abbiamo appena visto può essere usato, per analogia, per moltiplicare numeri vicini a potenze del 10. Per esempio, per moltiplicare per 99 basta moltiplicare per 100, aggiungendo due zeri, e quindi sottrarre il numero che stiamo moltiplicando, ad esempio per calcolare 45 × 99 basta prendere 4500 e sottrarre 45 ottenendo 4455 senza effettivamente svolgere nessuna moltiplicazione. Analogamente per moltiplicare per 57 × 1001 basta aggiungere 3 zeri e poi sommare 57, 57 × 1001 = 57000 + 57 = 57057.

Il trucco della moltiplicazione per 11

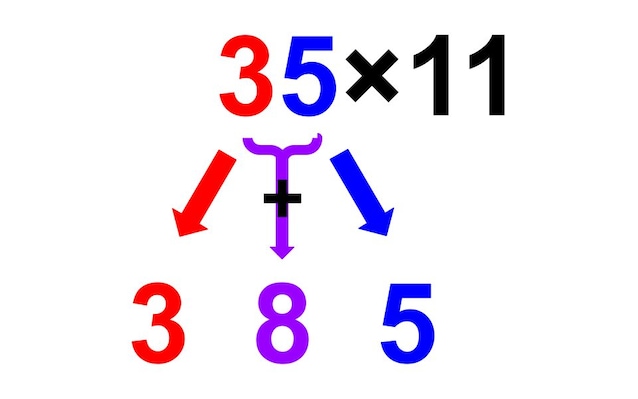
Le moltiplicazioni per 11 sono magiche, esiste infatti un modo super veloce per calcolarle senza svolgere neanche una moltiplicazione. Vediamolo con un esempio: per calcolare 35 × 11 si prendono come prima ed ultima cifra rispettivamente 3 e 5, e nel mezzo ci si mette la loro somma, 8, il risultato sarà quindi 385, come illustrato nella figura sotto.

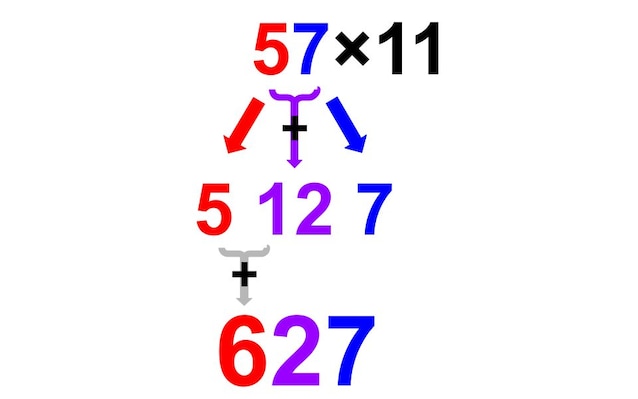
Le cose si complicano leggermente, ma non troppo, se la somma dei numeri è più grande i 9, ad esempio per calcolare 57 × 11, prendiamo 5 e 7 come prima ed ultima cifra e nel mezzo dovremmo a scrivere il risultato di 5 + 7 solo che questo fa 12: non c' problema, basta prendere 2 come cifra centrale e fare il riporto aggiungendo 1 alla prima cifra, quindi il risultato cercato sarà 627 (vedi figura sotto).

Sembra tutto facile se le cifre del numero che vogliamo moltiplicare per 11 sono solo 2, ma se sono di più? Questo trucco funziona lo stesso,  basta seguire questa procedura:

per moltiplicare un numero per 11 si prendono la prima e l’ultima cifra del numero come prima ed ultima cifra del risultato, mentre per determinare le cifre intermedie si prendono le somme delle cifre del numero di partenza, prese due a due, partendo dalle prime due fino alle ultime due, avendo cura di considerare tutti gli eventuali riporti.

Sembra proprio una magia, ma in realtà è solo matematica, proviamo a vederlo con il calcolo di 35×11: il numero 35 è formato da 3 decine e 5 unità, quindi 35 = 3 × 10 + 5, ed allo stesso modo 11 = 10 + 1, allora possiamo scrivere:

35 × 11 = (3 × 10 + 5) × (10 + 1) = 3 × 10 × 10 + 3 × 10 + 5 × 10 + 5 = 3 × 100 + (3 + 5) × 10 + 5 = 3 × 100 + 8 × 10 + 5.

Il passaggio finale ci mostra che alla fine ci sono 3 centinaia, 3+5=8 decine e 5 unità, ovvero 385.

Il metodo dei complementi alla base per i numeri vicini a 100

Supponiamo ora di voler moltiplicare tra di loro due numeri entrambi vicini a 100, ad esempio 94 × 97, non è un calcolo facilissimo da fare a mente, ma possiamo fare così:

1. si trova quanto dista ciascun numero da 100, nel nostro caso 100-94=6 e 100-97=3 (6 e 3 sono i complementi a 100 di 94 e 97)
2. si sottrae il complemento di un numero all’altro numero ad, esempio 94 – 4 = 91 (non importa quale numero si sceglie, il risultato sarà lo stesso infatti 97-6=91, in generale 91=100-6-3)
3. il numero che si ottiene, nel nostro caso 91, costituisce le prime due cifre del risultato della moltiplicazione.
4. si moltiplicano i due complementi tra di loro, nel nostro caso 6×3=18, trovando così le ultime due cifre del prodotto.
5. Si mettono insieme le cifre, in questo caso 9118.

Ma perché questo trucco funziona? Il fatto è che 94 = 100 – 6 e 97 = 100 – 3 per cui calcolare 94 × 97 è la stessa cosa che calcolare (100 – 6) × (100 – 3) e questo calcolo, grazie alla proprietà distributiva (che dice che a×(b+c)=a×b+a×c ed alla regola dei segni, può essere riscritto:

(100 – 6) × (100 – 3) = 100 × 100 – 100 × 3 – 100 × 6 + 6 ×. 3 = 100 × (100 – 3 – 6) + 6 × 3 = 100 × 91 + 18 = 9100 + 18 = 9118.

Nel calcolo si può vedere come sottraendo a 100 i due complementi, 6 e 3, si ottengono proprio le prime due cifre del risultato finale, mentre moltiplicandoli si ottengono le ultime due. Insomma, anche in questo caso non si tratta di magia ma di matematica.

Questo trucco, con dei piccoli accorgimenti può essere adattato a numeri poco più grandi di 100, ad esempio per calcolare 105 × 107 si scriverà 1 seguito dalla somma dei due complementi a 100, 5 e 7, quindi scriviamo 112 ed aggiungiamo come cifre finali il prodotto tra 5 e 7 ottenendo 11235 che è proprio il risultato di 105 × 107.

non perderti questo video

Il metodo giapponese per fare le moltiplicazioni è semplicissimo: ecco come farle