Come fanno le conchiglie ad avere la forma perfetta di una spirale: usano la matematica

Le conchiglie, con le loro forme affascinanti, sembrano essere disegnate da un abile scultore. Osservando una conchiglia da vicino, ci si rende conto che la sua spirale è una geometria incredibilmente precisa, come se fosse stata progettata con regole matematiche. Ma come è possibile che la natura crei qualcosa di così perfetto?

Com’è fatta una conchiglia e a cosa serve

Le conchiglie sono gusci protettivi che vengono costruite dai molluschi per proteggersi e sostenere il proprio corpo molle, che altrimenti sarebbe completamente esposto ai predatori o agli urti. La maggior parte della composizione di una conchiglia è fatta di carbonato di calcio, una sostanza minerale che costituisce circa il 95% del suo volume. Il restante 5% è composto da sostanze organiche, come proteine e altre macromolecole, che rendono la conchiglia flessibile, resistente e capace di crescere in modo continuo. Una delle caratteristiche affascinanti delle conchiglie è che non smettono mai di crescere. Quando il mollusco cresce, anche la sua conchiglia deve adattarsi alle nuove dimensioni. Questo processo avviene grazie al mantello del mollusco, lo strato più esterno, che secerne delle proteine che formano una sorta di impalcatura. Il carbonato di calcio si lega a questa struttura, creando nuovi strati che si aggiungono a quelli precedenti, mantenendo una crescita regolare.

È proprio questo ritmo regolare di crescita che dà forma alla spirale perfetta della conchiglia. Ma com'è possibile che cresca in questo modo così preciso?

La spirale di Fibonacci

La matematica entra in gioco: una delle forme più comuni che vediamo sulle conchiglie è la spirale logaritmica.

Prima di esplorare questo tipo di spirale, è utile parlare della successione di Fibonacci, una sequenza che inizia con 0 e 1, e dove ogni numero successivo è la somma dei due precedenti, partendo dai numeri iniziali 0 e 1 (0+1=1, 1+1=2, 1+2=3…). In questa sequenza il rapporto tra due numeri consecutivi tende all'infinito verso un valore fisso, circa 1,618. Questo numero è noto come sezione aurea, un valore che in matematica e nelle arti è associato alle proporzioni perfette. Costruendo dei quadrati il cui lato corrisponde a ciascun numero della sequenza di Fibonacci, si ottiene proprio una spirale. Questa è la spirale di Fibonacci, che somiglia a quella di una conchiglia, ma non è proprio così.

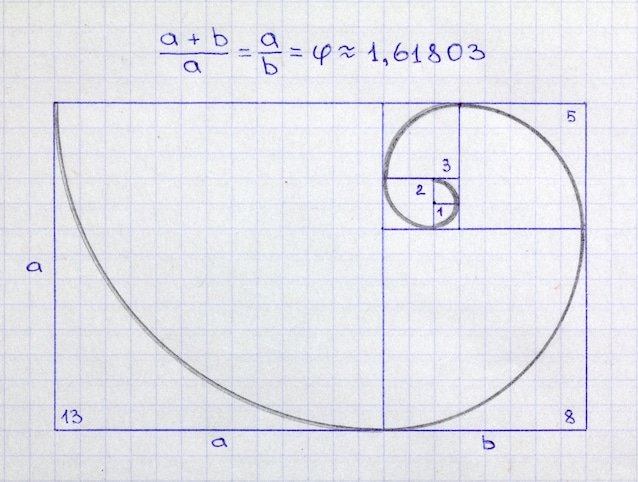
La spirale logaritmica

Le spirali delle conchiglie non sono tutte uguali, ma seguono la stessa struttura di una spirale di Fibonacci, almeno approssimativamente. La spirale di Fibonacci infatti è una buona approssimazione della spirale aurea, un tipo di spirale in cui il rapporto tra i raggi degli archi di circonferenza che compongono la spirale stessa è sempre uguale alla sezione aurea (1,618). La spirale aurea è a sua volta un tipo particolare di una categoria più ampia di spirali, le spirali logaritmiche.

La spirale logaritmica ha una proprietà unica: cresce mantenendo una proporzione costante, ma non necessariamente uguale alla sezione aurea. Man mano che la spirale si sviluppa, ogni giro si ingrandisce in proporzione al giro precedente, dando vita a una spirale che, pur ingrandendosi, mantiene sempre la stessa forma. E i molluschi fanno proprio così: aggiungono piano piano nuovo materiale, ma non lo fanno uniformemente, lo fanno in proporzione al materiale già presente, dando così vita a una spirale logaritmica precisa. Una delle caratteristiche di questa forma è la sua auto-similarità: non importa quanto ingrandisci o rimpicciolisci, la spirale rimane la stessa proprio per via delle proporzioni tra le sue parti che rimangono costanti per tutte le scale. In pratica, se osserviamo la conchiglia di un mollusco quando è molto piccola e quando è completamente cresciuta, la conchiglia apparirà identica nella sua forma generale, solo su una scala diversa, come se fosse stata “zoomata”.

La forma della spirale logaritmica non è solo esteticamente affascinante, ma anche estremamente funzionale. Crescendo in questo modo, la conchiglia non solo mantiene la sua forma, ma consente al mollusco di aggiungere nuovo materiale in modo efficiente, senza dover riprogettare continuamente la struttura. Questo permette al mollusco di crescere senza troppi sforzi, riducendo al minimo il consumo di energia.

Ma la spirale logaritmica non è un fenomeno esclusivo delle conchiglie. La si può osservare anche in altri contesti naturali, come nella traiettoria di volo del falco pellegrino, che durante la sua picchiata segue una spirale logaritmica per mantenere la preda nel suo campo visivo. Inoltre, il girasole organizza i suoi semi seguendo approssimativamente una spirale logaritmica, ottimizzando lo spazio sulla superficie del fiore.

In fin dei conti la matematica è ovunque. Le forme che si osservano in natura non sono casuali, ma seguono schemi precisi che permettono agli esseri viventi di crescere, muoversi e adattarsi in modo efficiente. La matematica è la lingua con cui la natura parla, e grazie ad essa è possibile leggere i suoi segreti. La bellezza della natura, quindi, non è solo estetica, ma è profondamente matematica.

non perderti questo video

Perché api e vespe costruiscono nidi a forma esagonale? La geometria delle celle