Il paradosso della bella addormentata: l’esperimento mentale

Il paradosso della bella addormentata è un dilemma che mette in discussione le nostre certezze sul calcolo delle probabilità. Immaginiamo questa situazione: la bella si addormentata di domenica e viene svegliata di lunedì o martedì in base al lancio di una moneta – se esce testa verrà svegliata di lunedì, se esce croce di martedì. Al suo risveglio le viene chiesto quanto ritiene probabile che sia uscita testa nel lancio della moneta. Sembra immediato pensare che la probabilità sia 50-50, perché le possibilità sono due: testa o croce. Eppure, se invece di concentrarci sulla moneta ci concentriamo sui possibili casi di risveglio, ci accorgiamo che diventano tre i casi possibili, e quindi la probabilità non è più del 50%!

Quale delle due letture è quella giusta? Non lo sappiamo: i matematici non hanno ancora trovato un accordo su questo paradosso. Vediamo i dettagli del dilemma e quali sono le principali correnti di pensiero sulla sua soluzione.

Il paradosso della bella addormentata e del lancio della moneta

La bella addormentata viene coinvolta in un esperimento in cui viene addormentata di domenica con un sonnifero per essere poi risvegliata di lunedì o di martedì a seconda dell'esito di un unico lancio di moneta. Le regole dell'esperimento sono queste:

1. se esce testa la ragazza viene svegliata di lunedì e le viene posta una domanda;
2. se esce croce la ragazza viene svegliata di lunedì, le viene chiesta la stessa domanda, quindi la si addormenta di nuovo con il sonnifero per svegliarla poi martedì e porle nuovamente la stessa domanda.

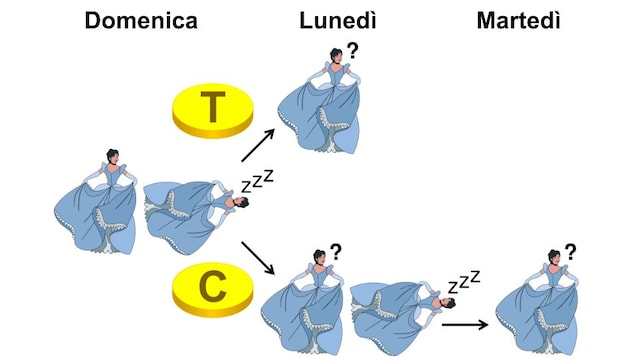
Teniamo presente che il sonnifero provoca una parziale perdita di memoria, per cui a ogni risveglio la bella addormentata non ricorda se è già stata svegliata in precedenza, ma ricorda le regole dell’esperimento. La domanda che le viene posta ad ogni risveglio è:

Quanto ritieni probabile che nel lancio della moneta sia uscita testa?

Sembra una domanda scontata: la moneta ogni volta può avere solo due esiti, testa o croce, e quindi la probabilità sarà del 50%. Eppure, nasce un dilemma probabilistico: se considerassimo non la variabile "moneta", ma la variabile "risveglio", i possibili casi diventano tre! E quindi la probabilità cambia. Vediamo perché.

Le due possibili soluzioni al paradosso della bella addormentata: qual è la probabilità?

La risposta più immediata a cui molti giungono è che la bella addormentata risponderà che la probabilità che sia uscita testa è il 50%, perché i possibili esiti della moneta sono solo due – testa o croce – e quindi ognuno dei due ha il 50% di probabilità di comparire, e per questo la prima soluzione è che la bella addormentata risponda:

La probabilità che durante l'esperimento sia uscita testa è il 50% .

Se però cambiamo punto di vista, le cose si complicano parecchio, ma soprattuto la risposta cambia! Invece di concentrarci sulla moneta infatti, ci concentriamo ora sui risvegli. Con questo cambio di prospettiva, il numero di esiti possibili cambia! Le situazioni in cui potrebbe trovarsi la bella addormentata al momento del risveglio non sono più semplicemente due, ma sono tre, perché nel caso dell'uscita della croce ci sono due possibili scenari, sia quello del lunedì che quello del martedì:

1. può pensare di essere stata svegliata di lunedì perché è uscita testa
2. oppure è stata svegliata di lunedì ma è uscita croce e verrà riaddormentata
3. infine, potrebbe trattarsi del risveglio martedì perché è inizialmente uscita croce

Questa volta i casi possibili sono 3, ma uno solo dei tre prevede che sia uscita testa, quindi secondo questa prospettiva, la probabilità che sia uscita testa è un caso su tre, ovvero 1/3 che scritto in percentuale è circa 33.33%. Secondo questo ragionamento quindi, la risposta della bella addormentata sarà:

La probabilità che sia uscita testa è 1/3, cioè circa il 33%

Entrambi i ragionamenti sono corretti, eppure danno risultati diversi! Ma quindi, la risposta giusta qual è? L’argomentazione che porta a concludere che la risposta giusta sia 1/3 è rafforzata dal filosofo della scienza Adam Elga che l’ha espressa in maniera formale utilizzando il calcolo della probabilità condizionata, un complicato modo di calcolare le probabilità quando un evento dipende da un altro evento. Ma, se ci pensiamo bene, la moneta potrebbe essere lanciata anche prima ancora dell’inizio dell’esperimento e non cambierebbe niente, per cui le probabilità che esca testa sarebbero comunque il 50% indipendentemente dai risvegli della nostra protagonista.

Insomma, è proprio un bel rompicapo, e infatti non sembra esserci un accordo definitivo sull’argomento, come testimoniato dal fatto che esistono decine pubblicazioni a supporto dell’una o dell’altra teoria.

non perderti questo video

Il paradosso del mentitore è il più antico del mondo: ecco cosa afferma