L’indovinello usato da Google per selezionare il personale: i prigionieri e i cappelli

L’indovinello dei prigionieri e dei cappelli è un famoso rompicapo logico, noto anche per essere stato utilizzato da Google nei colloqui di selezione del personale. L’obiettivo di questo test era valutare il pensiero logico dei candidati e capire chi tra loro fosse in grado di pensare fuori dagli schemi. Esistono diverse varianti, ma in tutte ci sono dei prigionieri condannati a morte, dei cappelli di cui non si conosce il colore e una potenziale strategia per riuscire a salvarsi.

In questo articolo vediamo la versione con dieci prigionieri, e solo cinque minuti per elaborare un piano.

L’indovinello dei dieci prigionieri e dei cappelli 

Dieci prigionieri sono stati rinchiusi in una prigione, in attesa di essere condannati a morte. All’improvviso, il carceriere offre loro una possibilità di salvezza proponendo una sfida: dice loro che tra cinque minuti saranno messi

non perderti questo video

Indovinello dei quattro cappelli: cos’è e come si risolve l’enigma dei 4 condannati a morte

in fila indiana, ordinati per altezza e rivolti in avanti. Chiunque provi a girarsi o a uscire dalla fila verrà giustiziato sul momento. A ciascuno verrà messo in testa un cappello, bianco o nero, scelto in modo casuale. Non sarà possibile sapere quanti cappelli ci sono di ciascun colore, né di quale colore sia il proprio cappello.

Quando il carceriere darà il via, ognuno dovrà indovinare il colore del proprio cappello, partendo dalla persona in fondo alla fila, quella più alta, e procedendo in ordine fino ad arrivare alla più bassa. Chi indovina il proprio colore verrà liberato. Chi sbaglia, verrà condannato.

Dice anche che potranno pronunciare solo la parola “bianco” o “nero”, senza aggiungere nulla e senza usare intonazioni strane o altri segnali. Qualsiasi tentativo di comunicare in altro modo porterà all’esecuzione immediata di tutti. Il carceriere concede 5 minuti ai prigionieri per discutere liberamente e provare ad elaborare una strategia. Come faranno a salvare il maggior numero di prigionieri?

La soluzione all’indovinello dei cappelli e dei prigionieri

Il destino dei prigionieri è nelle mani della persona più alta, quella in fondo alla fila. È l’unica che può vedere i cappelli degli altri nove e, quindi, dispone del maggior numero di informazioni. Se potesse semplicemente dire quanti cappelli neri e quanti bianchi vede, il problema sarebbe facilmente risolto. Ma può pronunciare solo una parola: “bianco” oppure “nero”.

Ai prigionieri, allora, viene un’idea brillante:

se la persona in fondo alla fila vede davanti a sé un numero pari di cappelli neri, dovrà dire “nero”; se vede un numero dispari di cappelli neri, dovrà dire “bianco”.

Grazie a questa strategia, riusciranno a salvarsi almeno 9 prigionieri su 10. Vediamo perché.

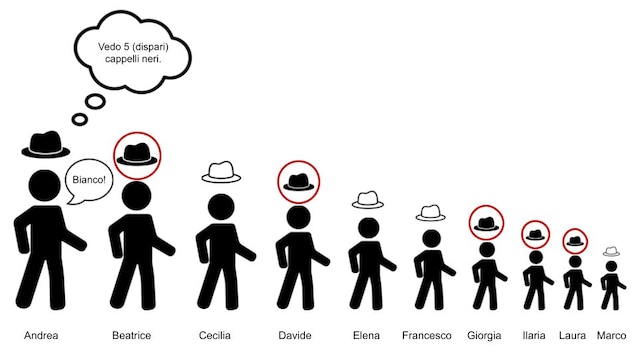
Se i prigionieri sono distribuiti come nell’immagine, il primo a parlare, che chiamiamo Andrea, vede davanti a sé cinque cappelli neri. Siccome cinque è un numero dispari, dice “bianco” ad alta voce, secondo la strategia concordata. Sbaglia il colore del proprio cappello, ma ora tutti sanno che i cappelli neri davanti a lui sono in numero dispari.

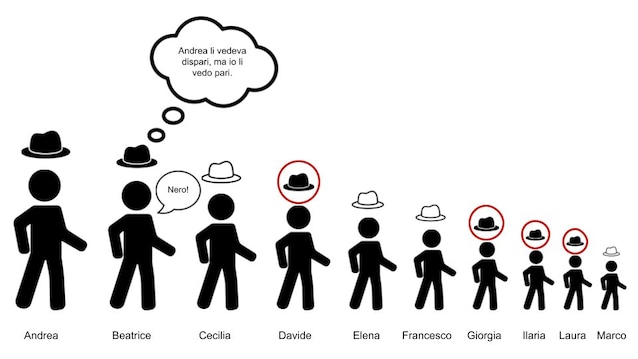
Ora tocca a Beatrice, la seconda della fila. Per capire di che colore è il suo cappello, Beatrice ragiona così:

Andrea ha visto un numero dispari di cappelli neri. Se anche io li vedo dispari, vuol dire che sto vedendo gli stessi cappelli neri che ha visto lui e quindi il mio dev’essere bianco. Se, invece, io li vedo pari, vuol dire che uno dei cappelli neri che Andrea ha visto dev’essere sulla mia testa. In quel caso, il mio cappello è nero.

Davanti a sé Beatrice vede quattro cappelli neri, cioè un numero pari. Sa quindi che il suo cappello è nero, lo dice ad alta voce e si salva.

Adesso, tutti i prigionieri sanno che i cappelli neri rimasti devono essere pari.

Una strategia quasi perfetta

Tocca quindi a Cecilia, la terza della fila, che davanti a sé vede un numero pari di cappelli neri, cioè quattro. Questo vuol dire che Cecilia e Beatrice vedono esattamente lo stesso numero di cappelli neri, e quindi Cecilia ha in testa un cappello bianco. Dichiara quindi “bianco” e anche lei si salva.

Ciascun prigioniero continua seguendo lo stesso tipo di ragionamento: parte aspettandosi di vedere un numero pari (o dispari) di cappelli neri, se il numero che conta è effettivamente pari (o dispari), significa che il proprio cappello è bianco. Se, invece, non corrisponde, allora è nero.

I prigionieri proseguono in questo modo fino ad arrivare agli ultimi due della fila, Laura e Marco, che hanno tenuto il conto di tutti i passaggi tra pari e dispari e sanno che Ilaria, la terzultima, ha visto un numero dispari di cappelli neri. Siccome Marco ha il cappello bianco, Laura dice a tutti che il suo cappello è nero. Marco, così, capisce che non sono rimasti più cappelli neri. Dice al carceriere che il suo cappello è bianco e anche lui riesce a salvarsi.

Questa strategia è la migliore possibile e funziona anche se aumentiamo il numero di prigionieri. La prima persona che parla ha il 50% di possibilità di sbagliare il colore del proprio cappello, ma grazie all’informazione che dà con la sua risposta, tutti gli altri prigionieri riescono a salvarsi.