Una scimmia instancabile che schiaccia tasti a caso può veramente scrivere la Divina Commedia?

Secondo il Teorema della scimmia instancabile, noto anche come Teorema delle scimmie infinite, se lasciassimo una scimmia premere a caso i tasti di una macchina da scrivere per un tempo infinito, prima o poi  finirebbe per digitare l’intera Divina Commedia o tutte le opere di Shakespeare. Insomma, il concetto è che avendo a disposizione un tempo infinito, la scimmia comporrebbe tutte le combinazioni possibili immaginabili sulla tastiera, e tra tutte queste combinazioni, ci sarà anche l'intera Divina Commedia.

Il primo a formulare questo teorema parlando proprio di scimmie fu, nel 1913, il matematico francese Émile Borel secondo cui:

Avendo a disposizione un tempo infinito, una scimmia che schiacci tasti a caso, prima o poi finirà per digitare qualsiasi testo o opera letteraria esistente o immaginabile.

Vediamo perché il teorema funziona dal punto di vista matematico della probabilità, e perché quando proviamo a metterlo in pratica, magari con scimmie vere, il teorema fallisce.

Perché il teorema della scimmia instancabile funziona?

Iniziamo con il cercare di capire come sia possibile che prima o poi una scimmia componga un manoscritto pigiando tasti a caso, partendo da un caso semplice.
Immaginiamo di voler scrivere la parola XY con una macchina da scrivere che ha solo due tasti, la lettera X e la lettera Y. Nell’immagine sotto possiamo vedere che schiacciando i tasti:

• 2 volte possiamo scrivere 4 parole di 2 lettere, di cui una sola è XY. La probabilità di successo è 1 su 4 ovvero il 25%.
• 3 volte possiamo scrivere 8 parole di 3 lettere, di cui la metà contiene XY. La probabilità di successo è salita al 50%.
• 4 volte possiamo scrivere 16 parole di 4 lettere, di cui 11 contengono XY. La nostra scimmia questa volta ha una probabilità del 68% di riuscire a digitare la parola XY.

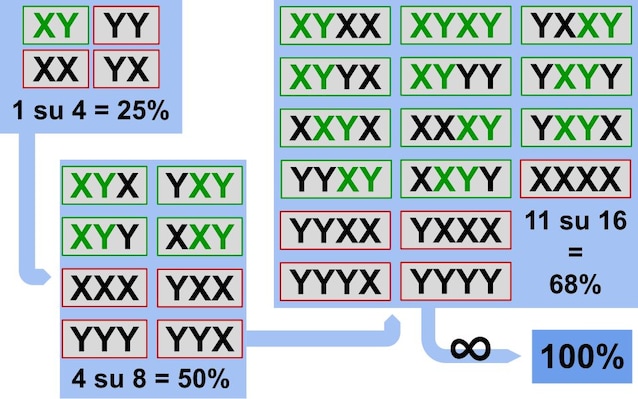
In pratica, aumentando il numero dei caratteri digitati, la probabilità di successo aumenta avvicinandosi sempre più al 100% e, per dirla in matematichese, al limite tende al 100% quando il numero dei caratteri tende ad infinito.

Se applichiamo lo stesso ragionamento al caso di una tastiera completa possiamo dedurre che la scimmia, avendo a disposizione un tempo infinito, prima o poi scriverà la Divina Commedia.

Il teorema messo in pratica: altamente improbabile e impossibile

Ma quanto quanto tempo può impiegare una scimmia a digitare un intero romanzo premendo tasti a caso?  È quello che si sono chiesti i matematici australiani Stephen Woodcock e Jay Falletta. I due ricercatori, ipotizzando che una scimmia digiti un tasto al secondo, hanno calcolato che

La probabilità che una scimmia riesca a scrivere la parola bananas nell’arco della vita media di una scimmia è circa il 5%.

Non è una probabilità alta, ma neanche bassissima, tuttavia Woodcock e Falletta hanno calcolato che cala drasticamente se vogliamo che la scimmia scriva l'intero romanzo Il pianeta delle scimmie: in questo caso la probabilità diventa un numero decimale piccolissimo con 698814 zeri dopo la virgola.

I due ricercatori si sono allora chiesti di quanto migliorerebbe la situazione impiegando un esercito di 200000 scimmie che digiti senza sosta fino alla morte del nostro universo, che si stima avverrà tra 10 alla 100 anni (un numero di 100 cifre). Anche in questo caso le probabilità di successo sono piuttosto basse, circa 0.0__06% con 15040 zeri dopo la virgola: è un numero talmente piccolo da far svanire qualunque speranza concreta di successo.

Per quanto riguarda la Divina Commedia, invece, i due ricercatori non se ne sono occupati, ma il testo scritto da Dante è un po’ più lungo del Pianeta delle scimmie (circa 100000 parole, contro 80000) e possiamo dedurre che la probabilità di successo sia ancora più bassa, quindi

è altamente improbabile che un esercito di scimmie possa scrivere la Divina Commedia prima della fine del nostro universo.

Insomma, sembra proprio che il teorema della scimmia instancabile non funzioni tanto bene nella realtà concreta, e c’è stato anche chi lo ha testato, con scarsi risultati, con le scimmie vere. Si tratta di un esperimento condotto dall’Università di Plymouth in cui 6 scimmie sono riuscite a produrre un testo di qualche pagina composto principalmente dalla lettera S. Il testo non contiene neanche una parola di senso compiuto, ma è stato comunque pubblicato online con il titolo di Notes towards the complete works of Shakespeare.

E quindi questo teorema funziona o no? Se pretendiamo di applicarlo ad una realtà concreta e finita il teorema non vale più, questo perché il passaggio dall’astratto della matematica al concreto del quotidiano non è quasi mai indolore: in questo caso specifico, quando passiamo dall'astratto al concreto, perdiamo come minimo la possibilità di effettuare infiniti di tentativi, che è uno degli aspetti chiave del teorema.

Tuttavia, se torniamo nel mondo immaginario della matematica tutto è possibile e, come ipotizzò Borel, la nostra scimmia, in un tempo sufficientemente grande, finirà davvero per scrivere qualsiasi cosa, anche questo articolo… e chissà che in realtà non sia stato scritto proprio da una scimmia?

non perderti questo articolo

Perché è impossibile pettinare una palla pelosa: la spiegazione del teorema