Moltiplicazioni egizie, il metodo che arriva dal 2000 a.C.: ecco come farle

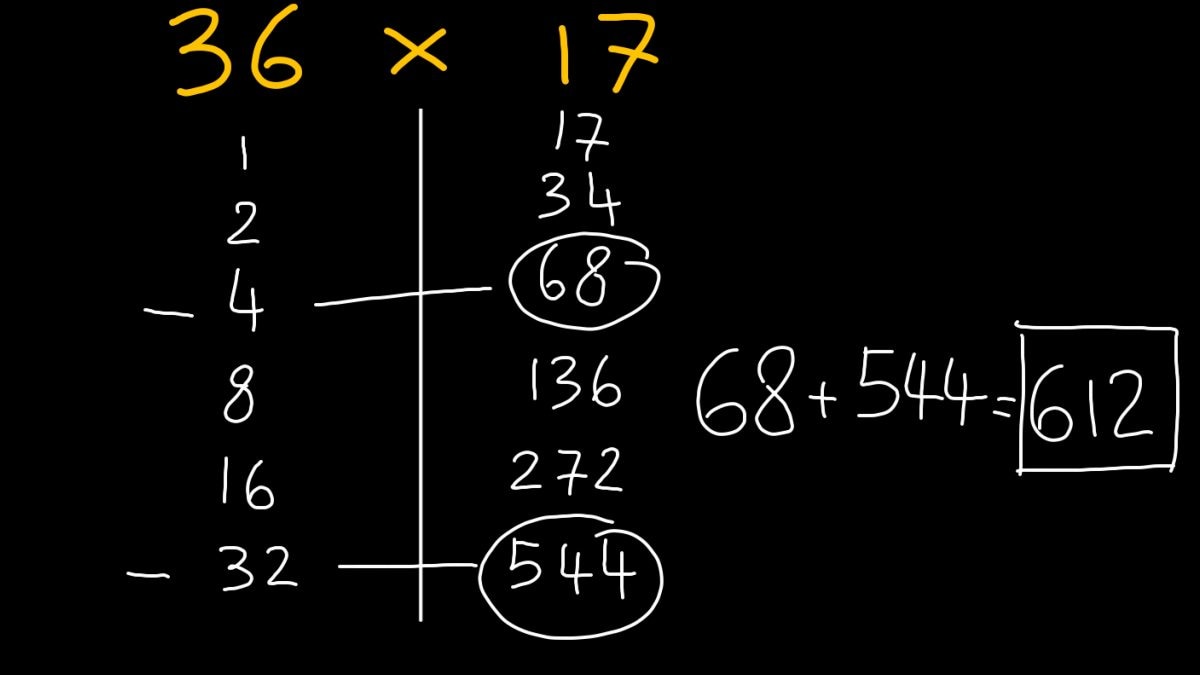
Se non abbiamo una calcolatrice con noi, il metodo più rapido che conosciamo per fare le moltiplicazioni è in colonna. Ma esiste un altro metodo risalente agli antichi egizi, arrivato a noi tramite un papiro del 1650 a.C., che si basa unicamente su raddoppio e somma.
Pur sembrando poco intuitivo, il metodo del raddoppio nasconde in verità diverse proprietà matematiche, tra cui la scrittura in binario di un numero e la proprietà distributiva della moltiplicazione.

Per moltiplicare basta raddoppiare

La moltiplicazione egizia, detta anche metodo del raddoppio, è arrivata ai nostri giorni grazie al ritrovamento del papiro di Rhind, uno scritto risalente al 1650 a.C., quando lo scriba Ahmes trascrisse un papiro precedente del 2000 a.C. contenente tabelle di frazioni e problemi aritmetici, algebrici e geometrici.

Il metodo è molto semplice, anche se non immediato, e consiste nell'esecuzione di due differenti raddoppi ripetuti:

non perderti questo video

Il metodo giapponese per fare le moltiplicazioni è semplicissimo: ecco come farle

• il primo, sotto il primo fattore della moltiplicazione, consiste nel partire da 1 e raddoppiare – quindi si prosegue con 2, poi 4, 8, 16, … – fino ad arrivare alla più grande potenza di 2 inferiore al primo fattore (nel caso dell'esempio sotto, essendo il primo fattore uguale a 36, la più grande potenza di 2 minore di 36 è 2⁵ = 32)
• il secondo, sotto il secondo fattore della moltiplicazione, consiste nel partire dal valore del fattore (nel caso dell'esempio sotto, 17) e raddoppiare – quindi nel nostro caso 17, 34, 68, … – tante volte quante sono i raddoppi della prima colonna.

A questo punto, scegliamo sotto il primo fattore i numeri che, sommati, danno come risultato proprio il primo fattore (nel nostro caso, scegliamo 32 e 4, che sommati danno 36). Siamo sicuri che questa operazione sia fattibile perché è proprio la scrittura in binario del primo fattore e ogni numero intero può essere scritto come somma di potenze di 2.
Adesso scegliamo i corrispondenti numeri che troviamo nella colonna sotto il secondo fattore e li sommiamo. La loro somma è proprio il risultato della moltiplicazione (nel nostro caso, sono 68 e 544, che sommati danno 612, che è proprio il risultato dell'operazione 36 x 17 – provare con la calcolatrice per credere!).

Il metodo usa la scomposizione in binario e la proprietà distributiva

A vederla così, sembra incredibile che questo metodo apparentemente casuale ci dia proprio il risultato della moltiplicazione. In verità, quello che si nasconde alle sue spalle è qualcosa di molto sofisticato, cioè il sistema binario, che sta alla base dell'informatica moderna.

Quando scriviamo sotto il primo fattore le potenze di 2 e poi scegliamo quelle che, sommate, danno come risultato il primo fattore, stiamo proprio scomponendo il numero nelle sue componenti binarie. Nel nostro caso, abbiamo scritto 36 come 4+32, cioè 2²+2⁵. Senza saperlo, nella seconda colonna abbiamo scritto proprio le potenze di 2 che vediamo nella prima colonna, moltiplicate per il secondo fattore, quindi nel nostro caso 17.

Quando andiamo a sommarli, quindi, stiamo sostanzialmente utilizzando la proprietà distributiva: abbiamo scomposto il primo fattore in potenze di 2, e poi invece di moltiplicare il primo fattore per il secondo, abbiamo moltiplicato le varie potenze di due per il secondo fattore, per poi sommare il risultato.