Perché quando pieghiamo una fetta di pizza la punta non si piega all’ingiù: è una questione matematica

Se la punta della fetta non scende una volta piegata la fetta è per via del Theorema Egregius di Gauss sulla curvatura delle superfici.

Vogliamo andare oltre il web: partecipa alla Missione Cultura

A cura di Michele Cerulli

Avete mai notato che quando piegate a U una fetta di pizza la punta non scende praticamente mai verso il basso, mentre lo fa quasi sempre se non piegate la fetta? Il motivo non risiede in qualche considerazione fisica ma è un esempio di un risultato matematico legato alla curvatura di superfici: stiamo parlando del Theorema Egregium del genio matematico Carl Friedrich Gauss, che dimostra come non possiamo piegare una superficie come vogliamo se non vogliamo rischiare di romperla. Vediamo cosa dice il teorema e come può aiutarci a mangiare la pizza, passando per patatine, banane ed arance.

Cos'è la curvatura di una superficie dal punto di vista matematico (e cosa c'entra con la pizza)

Tanto per cominciare i matematici vedono la pizza come una superficie, ovvero un oggetto di dimensione due, che può essere piatto come un foglio di carta oppure avere una forma incurvata come la patatina della figura sotto che si incurva sia verso l’alto che verso il basso.

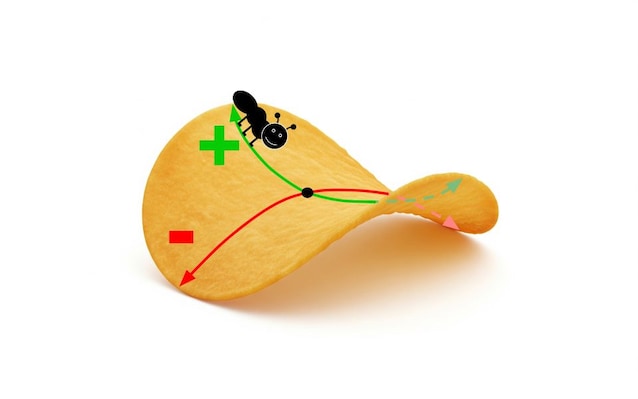
Prendiamo il punto centrale della patatina e immaginiamo una formichina che cammini dritta da un'estremità alta della patatina fino all'altra estremità alta passando proprio per quel punto. Anche se la formichina cammina dritta, noi da fuori la vediamo percorrere una linea curva, come quella verde della figura sopra. Lo stesso accade se la formichina si cammina dritta da un'estremità bassa della patatina all'altra, percorrendo la linea curva rossa della figura. Le due curve tracciate dalla formichina si incontrano in un punto ma non sono uguali: una è rivolta verso l'alto e l'altra verso il basso. Per distinguerle, come fanno i matematici, possiamo dire che una delle due è negativa e l’altra è positiva (no, non è una questione di alto basso e in questo caso specifico potremmo invertire i due segni, basta che siano diversi tra loro).

Ogni volta che la formichina cammina su una superficie percorre una linea incurvata, tanto o poco, in un verso o nell'altro, a seconda della forma della superficie. Nella figura sotto vediamo il caso di un'arancia in cui le due linee sono entrambe positive perché entrambe incurvate verso il centro dell'arancia, le due curve sono abbastanza simili, ma questo non è il caso di quelle tracciate dalla nostra formichina sulla banana.

Nel caso di una banana, infatti, abbiamo un punto in cui le due linee che si incrociano hanno segno opposto, ma questa volta la linea negativa è molto più incurvata di quella positiva, possiamo vederla come pezzo di una circonferenza piccola piccola, mentre la linea positiva sembra un pezzetto di una circonferenza molto più grande. Per descrivere quanto è curva una linea i matematici fanno riferimento alla lunghezza dei raggi di queste circonferenze immaginarie, riuscendo quindi a descrivere la curvatura di una linea con un numero, che può essere positivo o negativo, grande o piccolo.

C'è un problema, però, se prendiamo un punto su una superficie, come per la banana della figura sotto, possiamo tracciare (sempre andando dritti come una formichina!) tante linee diverse, che in generale possono essere più o meno curve.

Ma allora, se vogliamo stabilire di quanto è incurvata la banana in quel punto, quali di queste linee dobbiamo considerare? Ce ne sono infinite, mica possiamo analizzarle tutte! L’intuizione del matematico tedesco Carl Friedrich Gauss (1777-1855) è stata che basta sceglierne due, la linea con la curvatura maggiore e quella con la curvatura minore, e moltiplicare tra di loro le due curvature, ottenendo quindi un singolo numero per ogni punto della superficie detto curvatura di Gauss.

Con questa possiamo stabilire facilmente se una superficie ha una curvatura positiva, negativa o nulla. Ad esempio, nel caso della patatina, poiché vi sono sia linee con curvatura positiva che linee con curvatura negativa, la curvatura di Gauss nel punto considerato è negativa perché, si calcola moltiplicando tra loro un numero negativo ed uno positivo, e come si sa "più per meno fa meno". Lo stesso vale per il punto che abbiamo preso sulla superficie della banana. Per quanto riguarda l’arancia invece, abbiamo una curvatura di Gauss positiva visto che tutte le linee hanno curvatura positiva.

Il caso più facile è quello delle superfici piatte, come un tavolino o un foglio di carta, qualunque linea tracciamo andando dritti (si, sempre camminando come una formichina) questa risulta dritta anche vista dall’esterno e per tanto la sua curvatura è nulla, di conseguenza la curvatura di Gauss di un foglio o di un tavolino è proprio 0: chi se lo sarebbe mai aspettato?

Cosa dice il Theorema Egregium di Gauss

Bene, abbiamo visto cosa è la curvatura di Gauss, ma questo ancora non ci dice perché la pizza non crolla all’ingiù quando la pieghiamo. Ci viene di nuovo in aiuto Gauss, che ha dimostrato un teorema, da lui stesso definito Theorema Egregium, secondo cui

se pieghiamo una superficie senza strapparla, senza allungarla e senza rimpicciolirla, la sua curvatura di Gauss non cambia

Dal punto di vista concreto il teorema ci dice che se proviamo a schiacciare la patatina sul tavolino questa deve necessariamente rompersi: la patatina infatti ha curvatura negativa, se potesse appiattirsi sul tavolino la sua curvatura dovrebbe diventare zero, ma questo, secondo il teorema, non può accadere a meno che non vi siano delle rotture. Ed ecco che possiamo finalmente spiegare cosa succede con la pizza.

Come il teorema di Gauss ci aiuta a mangiare la pizza

Una fetta di pizza può essere vista come una superficie triangolare piatta, quindi in ogni suo punto la sua curvatura di Gauss vale zero. Quando solleviamo la fetta tenendola semplicemente dal bordo questa si piega immancabilmente verso il basso, ma questo non contraddice il Theorema Egregium perchè la curvatura rimane zero: la linea che segue la piega ha curvatura zero, mentre tutte le altre sono positive, e zero per un numero positivo fa sempre zero (vedi figura sotto).

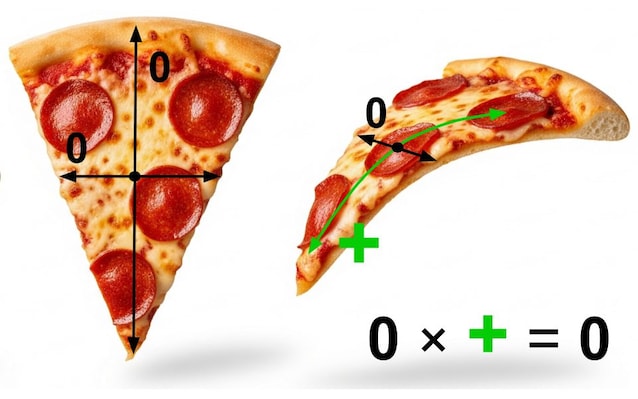
Analogamente anche quando pieghiamo i bordi della pizza verso l’alto la curvatura di Gauss rimane zero: per i punti della parte incurvata passa una linea dritta, con curvatura zero, e molte linee incurvate verso l’alto con curvatura negativa (vedi figura sotto), per cui il prodotto continua a valere zero. Ora, se la pizza si piegasse anche verso il basso, verrebbe a crearsi almeno un punto per il quale passano sia linee incurvate verso l’alto che linee incurvate verso il basso e la curvatura di Gauss diventerebbe negativa ("più per meno fa meno"!): questo per il Theorema Egregium è impossibile, a meno di strappi, e infatti se proviamo a farlo la pizza si strappa!