Perché l’identità di Eulero è considerata l’equazione più bella della matematica

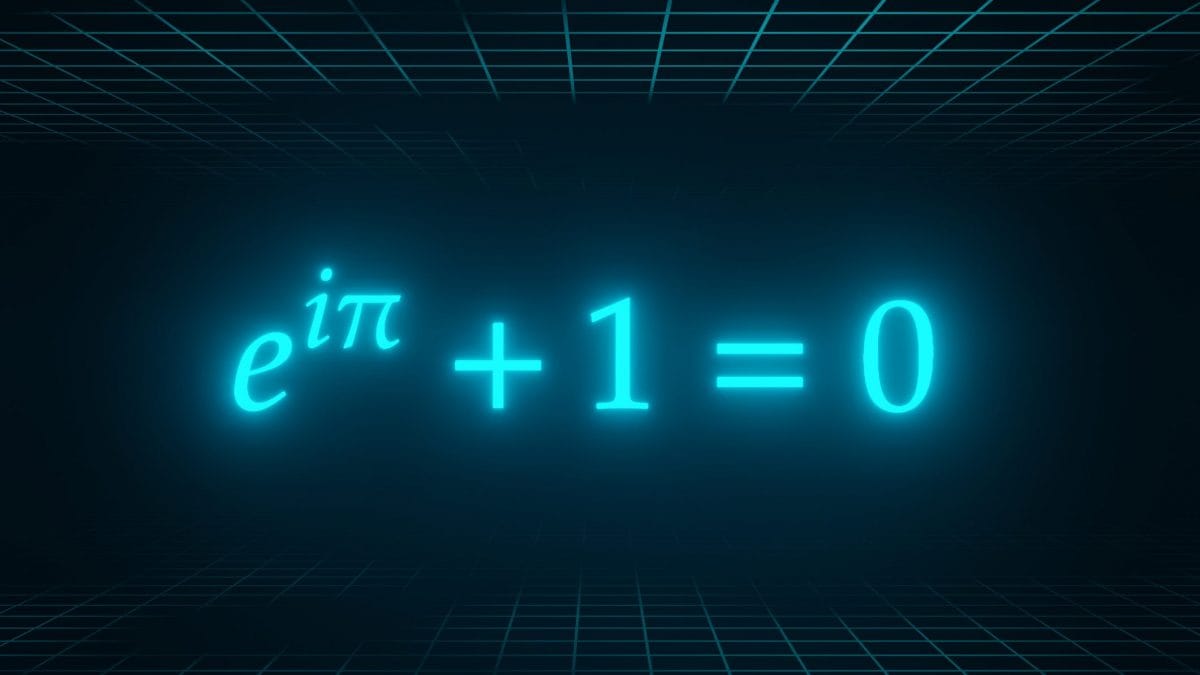
La formula e^iπ + 1 = 0, detta identità di Eulero, ci parla di potenze e numeri complessi ed è da molti considerata l’equazione più bella del mondo. Ciò che la rende così affascinante agli occhi dei matematici è la sua capacità di mettere insieme cinque dei più importanti numeri della matematica. Vediamo cosa ci dice questa formula, scoperta dal matematico svizzero Eulero nel 18° secolo, cosa c'entra con potenze e numeri complessi e perché è collegata anche alle funzioni delle onde ed alla crescita esponenziale.

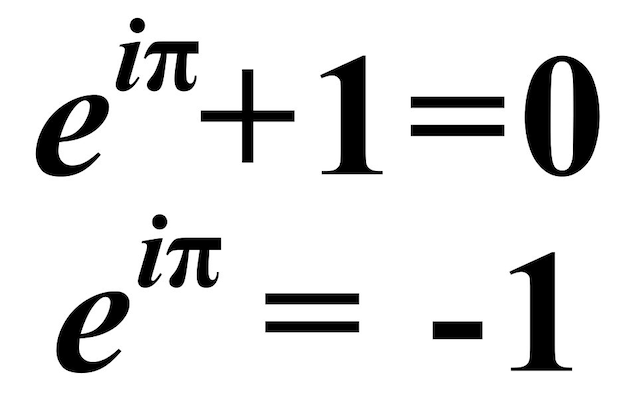
L'identità di Eulero (vedi figura sopra) è una formula che si occupa di potenze e numeri complessi mettendo insieme alcune delle più importanti e famose costanti matematiche. Ed è proprio grazie alla sua capacità di legare indissolubilmente i seguenti numeri che molti studiosi la ritengono una delle più belle formule della matematica:

• la costante matematica e, nota anche come numero di Nepero, che vale circa 2.71 
• π, che vale circa 3,14, al quale è stato addirittura dedicato un giorno dell'anno, il Pi greco day.
• i, uno strano numero che appartiene al mondo dei numeri complessi, che è la radice quadrata di -1.
• il numero 0, l'elemento neutro della somma
• il numero 1, l'elemento neutro della moltiplicazione

I protagonisti dell'identità di Eulero sono tutti numeri con valori bene determinati, anche se sono indicati tramite lettere, per questo è più corretto chiamarla identità piuttosto che equazione, e volendo possiamo riscriverla senza usare neanche una lettera, come nella figura sotto, ma a patto di usare il simbolo ≅ per specificare che stiamo approssimando i valori di e e π.

non perderti questo articolo

Perché in matematica si usa la “x” per indicare un’incognita?

Di Maria Bosco

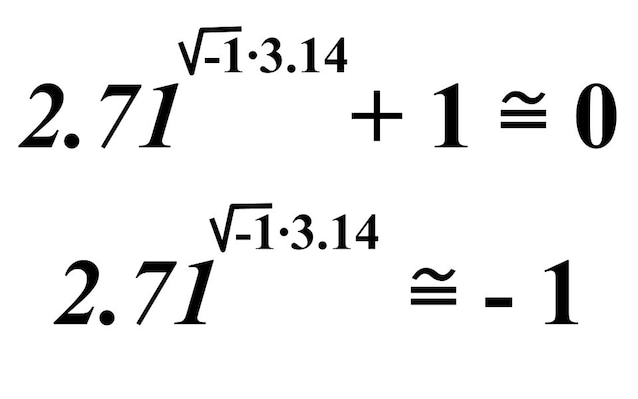
Solitamente la si lascia scritta in lettere in maniera da non incappare in approssimazioni, ma scriverla usando i numeri ci aiuta a capire che, in fondo, questa formula non ci dice altro che il risultato di una particolare potenza la cui base è il numero e (≅2.718) e il cui esponente è il prodotto tra π (≅ 3.14) ed il numero Complesso i (la radice quadrata di -1). Quindi questa identità è sostanzialmente il calcolo di una potenza, ma non è una potenza qualsiasi, bensì è una potenza con un esponente speciale, un numero Complesso.

Quando parliamo di numeri complessi ci riferiamo ad un'estensione dei numeri Reali (i numeri decimali che tutti conosciamo). La particolarità di questi numeri è che alcuni di loro, quando sono elevati alla seconda, danno come risultato un numero Reale negativo. Questo è quello che accade al numero i, per il quale vale i × i = -1, ed a tutti i sui multipli, che vengono chiamati numeri Immaginari. Ogni numero Complesso è la somma di un numero Reale, detto parte Reale, e di un numero immaginario, detto parte Immaginaria. Ad esempio 3+4i è un numero complesso con parte reale 3 e parte immaginaria 4.

Il calcolo delle le potenze con i numeri complessi non è semplice e può dare sia risultati Reali, che Immaginari, che una combinazione dei due. Tuttavia, Eulero stesso ha enunciato un'altra formula molto importante (vedi immagine sotto), grazie alla quale è riuscito a ricavare proprio l'identità di Eulero che possiamo usare per calcolare alcune potenze, compresa quella della nostra identità.

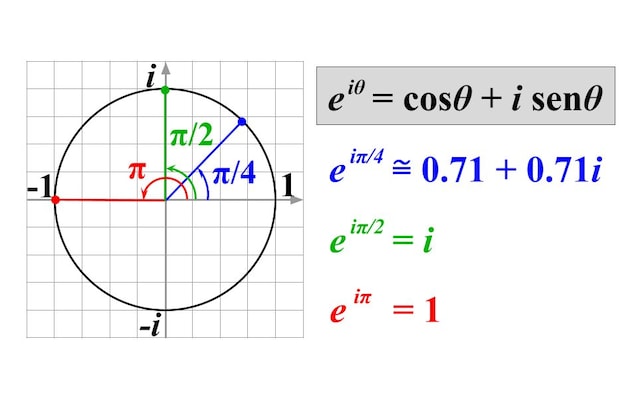
Come possiamo vedere, e elevato alla iπ/4 risulta in un numero complesso composto sia da una parte reale (circa 0.71) che da una parte immaginaria (circa 0.71i), mentre e elevato alla iπ/2 è uguale al numero immaginario i, senza parte Reale. Può capitare, infine, che il risultato sia un numero puramente Reale, come nel caso di e elevato alla iπ che è uguale a -1, come stabilito dall'Identità di Eulero. 

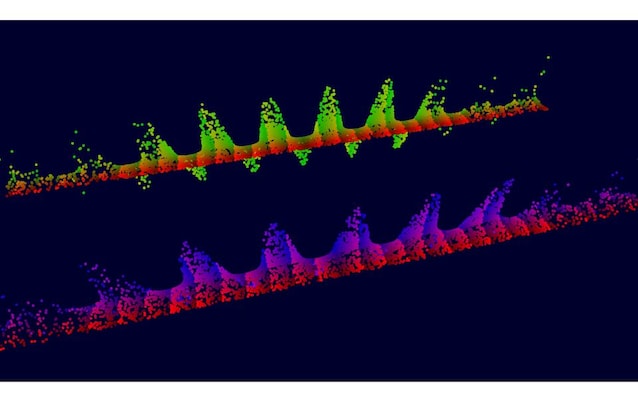
Questa formula, infine, nasconde in se un altro piccolo gioiello che dona un ulteriore tocco di fascino all'identità di Eulero. Come si può vedere dalla figura sopra, nella formula compaiono anche le due funzioni trigonometriche seno e coseno (indicate come sen e cos), che servono a descrivere le onde e che in questa formula vengono associate al concetto di potenza nella sua forma più generalizzata che prende il nome di funzione esponenziale. L'Identità di Eulero, quindi, è anche figlia di una formula capace di mettere insieme fenomeni ondulatori e crescite esponenziali, un piccolo tocco di fascino in più che possiamo visualizzare con una rappresentazione tridimensionale delle parti Reale ed Immaginaria delle potenze di e.