
Negli ultimi decenni, lo sviluppo tecnologico e la possibilità di raccogliere quantità enormi di dati hanno cambiato il modo in cui osserviamo il mondo. Oggi disponiamo di reti che possono contenere milioni di elementi in interazione: reti di persone, reti digitali, reti biologiche, reti infrastrutturali.
Questi sistemi mostrano comportamenti non intuitivi, difficili da prevedere studiando solo le loro parti singole. Per comprenderli serve un approccio diverso, ovvero la teoria delle reti (o network theory), basata sugli strumenti matematici della teoria dei grafi. Vediamo di cosa si tratta e perché è importante per capire i sistemi complessi.
Dai grafi alle reti complesse: a cosa servono queste strutture
In matematica, un grafo è una struttura composta da punti o nodi (gli elementi) e linee (le relazioni tra elementi). È un modello molto semplice, ma incredibilmente efficace per rappresentare sistemi complessi.
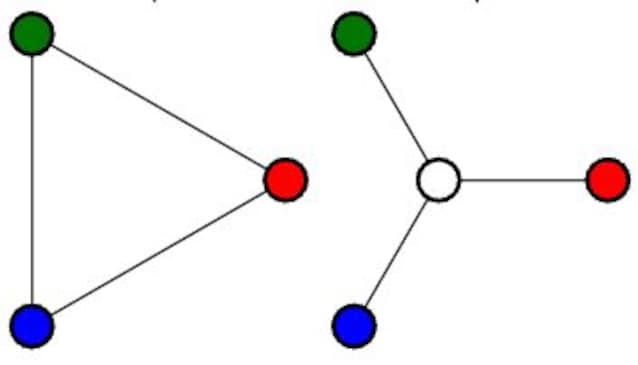
Nonostante la loro semplicità, i grafi permettono di estrarre in modo sintetico e oggettivo informazioni da reti enormi, impossibili da analizzare nel dettaglio elemento per elemento.
Ed è proprio questo uno dei punti cruciali della scienza delle reti: non basta conoscere tutte le parti di un sistema per comprenderlo, perché il comportamento complessivo dipende soprattutto da come quelle parti interagiscono.
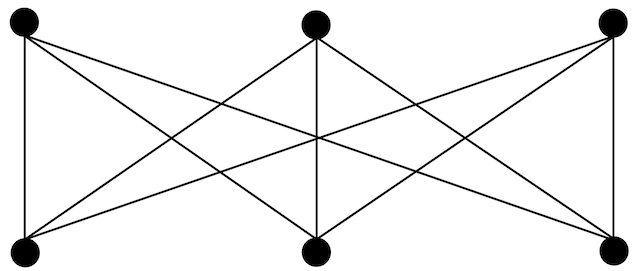
Questo rappresenta un superamento del tradizionale approccio riduzionista, secondo cui conoscere ogni singolo pezzo dovrebbe bastare per capire il tutto. Nei sistemi reali non è così: un sistema complesso non è la semplice somma delle sue parti, ma è il risultato delle loro connessioni.
Perché guardare alle connessioni cambia tutto
La teoria delle reti permette di ricostruire la mappa delle interazioni all’interno di un sistema: prima si studia la sua architettura — nodi e connessioni — poi si analizzano le dinamiche che si propagano attraverso quei collegamenti.

È esattamente il motivo per cui fenomeni molto diversi tra loro possono essere studiati con gli stessi strumenti matematici: la diffusione di segnali elettrici nei neuroni, la propagazione di un’informazione sui social network, l’effetto domino causato dal ritardo di un grande aeroporto, la trasmissione di un virus respiratorio all’interno di una popolazione.
Questi sistemi appartengono a campi diversi — biologia, tecnologia, trasporti, sociologia — ma condividono proprietà strutturali comuni. È uno dei risultati più importanti della scienza delle reti: molti sistemi complessi funzionano secondo le stesse regole matematiche.
Cosa rende una rete “reale”
Nell’osservazione di reti reali — biologiche, tecnologiche, ecologiche o sociali — emergono quattro caratteristiche ricorrenti:
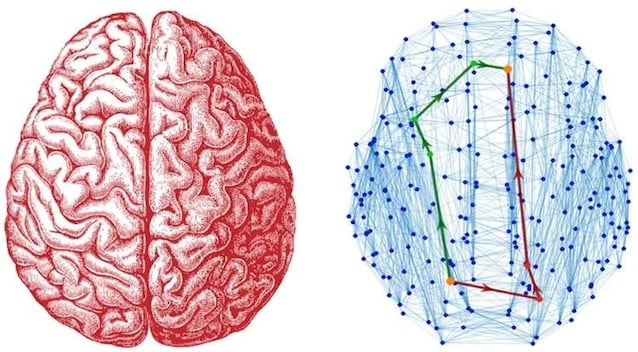
- Alto clustering. I nodi tendono a formare gruppi locali molto connessi. È il fenomeno per cui gli “amici dei miei amici” spesso sono tra loro collegati. Lo stesso accade nei neuroni di una stessa area corticale o tra aziende dello stesso settore.
- Piccole distanze di rete. Tra due nodi qualsiasi esistono in media pochi passaggi. Ad esempio, nella corteccia cerebrale questo si traduce in percorsi di comunicazione rapidi tra regioni distanti.
- Distribuzione diseguale delle connessioni. In molte reti, pochi nodi accumulano un numero molto alto di collegamenti — gli hub — mentre la maggior parte dei nodi ne ha pochi. Questo vale per aeroporti globali (es. Atlanta, Dubai, Heathrow), per pagine web, per specifiche aree del cervello.
- Dinamismo. I nodi possono nascere, crescere e scomparire, ma la struttura complessiva della rete rimane stabile. Queste proprietà collocano le reti complesse in una zona intermedia tra sistemi completamente ordinati e sistemi completamente casuali.
I modelli fondamentali della scienza delle reti
Negli anni ’90 due modelli matematici hanno rivoluzionato la comprensione delle reti reali: si tratta del modello Small-World (Watts & Strogatz, 1998), il quale mostra che è possibile avere contemporaneamente: forti connessioni locali (alto clustering), brevi distanze globali tra nodi lontani. Insomma, bastano poche “scorciatoie” per rendere il mondo sorprendentemente piccolo.
Il secondo è il modello Scale-Free (Barabási & Albert, 1999), che rivela come la distribuzione delle connessioni in molte reti segue una legge di potenza: pochi nodi hanno moltissime connessioni e la maggior parte hanno pochi collegamenti. Questo accade perché le reti reali crescono nel tempo e favoriscono i nodi già molto connessi (attaccamento preferenziale). Questo è il meccanismo alla base della crescita del Web, dei social network e di molte reti biologiche.
Perché la scienza delle reti è diventata centrale
Oggi la network science viene applicata in campi sempre più diversificati:
- epidemiologia: per modellare la diffusione di malattie;
- ingegneria dei trasporti: per progettare reti più robuste;
- informatica: per comprendere il funzionamento di Internet, del Web, per l'intelligenza artificiale;
- neuroscienze: per studiare la connettività cerebrale e i cambiamenti dopo traumi;
- economia: per analizzare sistemi finanziari e catene di fornitura;
- ecologia: per mappare relazioni tra specie e flussi energetici.
La forza di questo approccio sta nel fatto che consente di descrivere sistemi estremamente complessi attraverso proprietà comuni, indipendentemente dalla natura dei loro componenti. Per questo Barabási ha definito la scienza delle reti come “la prossima rivoluzione scientifica”: un nuovo punto di vista che permette di comprendere l’organizzazione profonda dei sistemi reali.
;Resize,width=767;)



;Resize,width=727;)

;Resize,width=727;)

;Resize,width=727;)

